子空间
以下等价
- not co-linear
if , 可能
-
2 time(-like)
Example, where
可以线性生成 - 1 time, 1 space
Example - 1 time, 1 null
Example - 2 null
Example . 注意 . signature - 2 space.
Example
, where - other cases (symmetry of time space)
考虑一般的 中的
[signature-of-2d-subspace-of-spacetime] Prop Minkowski 在 的 的可能 signature 是
Prop time-like 只正交于 space-like
let time-like. 使用正交分解, let then ==> space-like
Prop light-like 不正交于
- time-like
- 与自身共线 之外的 light-like [metric-cannot-distinguish-colinear-light-like]
根据情况取一个正交分解
- time-like ==> let ==>
- light-like
我们证明
but
space-like 但长度零, 所以
==>
Prop 的二维子空间的 signature 不可能是 or
Proof 用上一个定理
Prop 的两个不共线 time-like 的展开 的 signature 是
Proof 以其中一个为初始的基来生成 正交基, 但 signature 不能是 , 所以只能是
的射影
Prop let , let time-like or light-like with 不共线. 则
Proof
已知
在光锥上等价于解变量 的二次方程
Prop 的两个不共线 light-like 的展开 的 signature 是 or
Proof Euclidean 没有 light-like, 所以无其它可能性
Example
- 的
- 的 . 相减得到正交基
[simultaneity-relativity] 相对论同时性
use 正交基延拓
in , space-like 子空间的正交补是 time-like 子空间
-
( space-like <==> 存在 time-like 同时正交于 )
-
( not space-like <==> 不存在 time-like 同时正交于 space-like )
直观: 不同 space-like 子空间 无法使用兼容的时间计算方式 or 的 time-like 正交补不相同
use 正交分解
分类讨论 . 内积的时间相乘的符号决定内积的符号
分类讨论 . 内积的空间相乘的符号决定内积的符号
in Euclidean, we have 内积不等式 ==> 三角不等式
in signature 二次型, 这一般不成立
将 二次型 导出 到交错二阶线性
[quadratic-form-inequality-Minkowski] 内积不等式
in , let not co-linear, so
二次型限制在 上, signature
- ==> ==>
- ==> ==>
Proof
==>
二次型导出到
signature
-
of ==> of
Proof
of 正交基 , ==> 正交基 ,==> , i.e. 内积不等式
-
of ==> of
==>
[triangel-inequality-Minkowski] 三角不等式
- 2 time
,
- ==>
- ==>
- 1 time, 1 null
==>
- ==>
- ==>
Proof of 2 time-like
Euclidean 空间已经可以讨论不同的收敛方向 e.g. 序列 是否收敛到 . 螺旋线 like 的东西在方向空间不收敛
Euclidean 空间在所有 方向收敛到一点 <==> 在所有方向一致地收敛到一点, by compactness of
Minkowski 空间方向空间 is non compact. 虽然我们尚未定义 的网
Minkowski 空间的 net 需要足够远离光锥
let
对于收敛的类时方向, 可以分开
- 未来:
- 过去:
- 混合: quotient 掉双叶 , 成为 projective space 式的方向空间
in
let
[hyperbolic-complex] 双曲复数. cf. split-complex-number
- 按分配率展开
[hyperbolic-exp]
use 二项式
-
-
-
, . by
[polor-coordinate-hyperbolic]
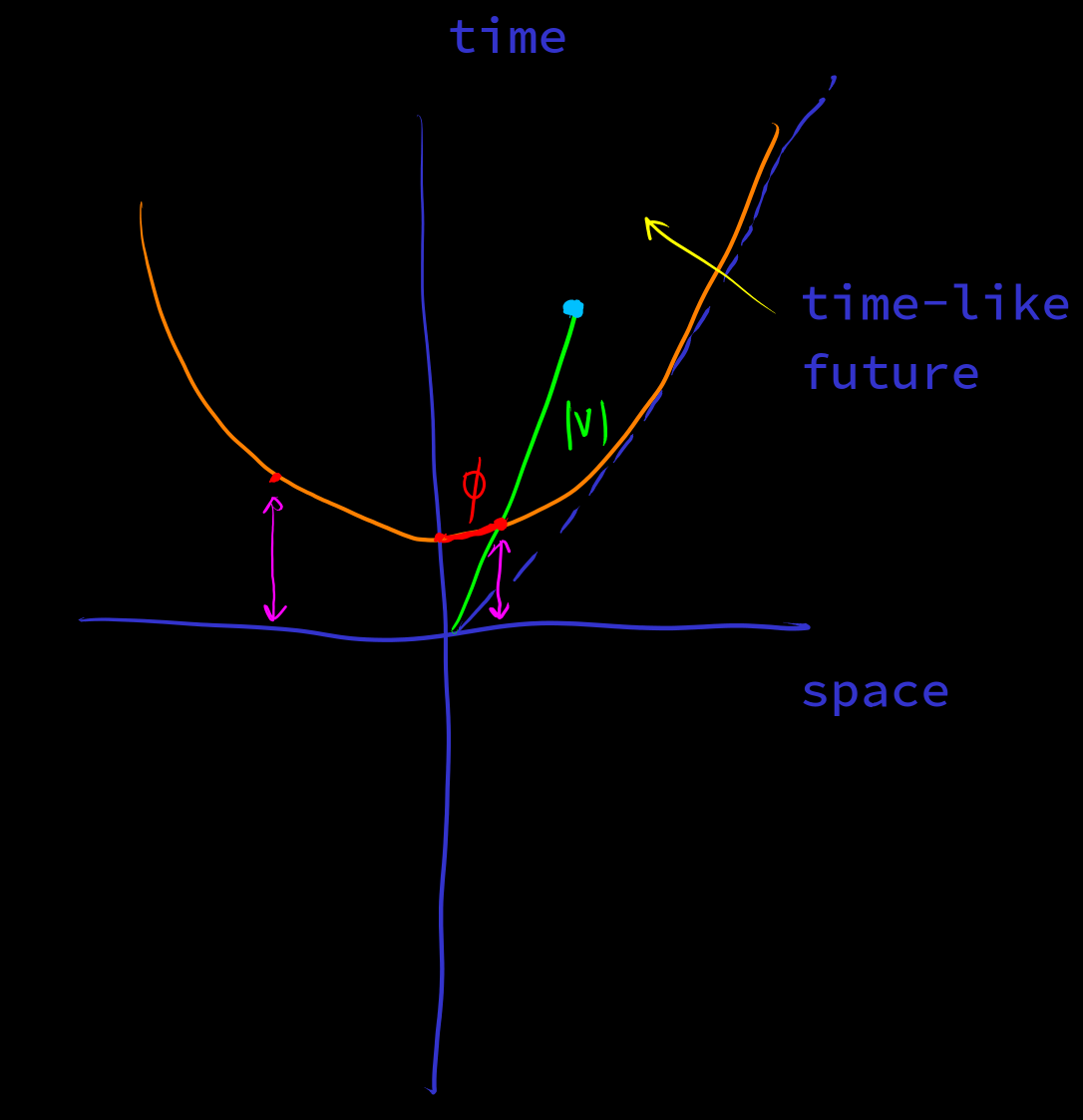
双曲极坐标 , , . can come from 测地线长度参数. 也称为双曲角度 [hyperbolic-angle]
极坐标即距离和方向的分解
不是 测地线长度, 而是 的长度
[hyperbolic-isom]
group isomorphism (比较复数的情况)
单调递增
解二次方程 得到逆映射
inverse
Question 模仿 用球极投影和 , 用 双曲投影 和 来处理双曲角度 or 测地线长度映射
的测地线坐标就是
记号冲突. 测地线坐标也通常用记号 , 但不是用 代数去定义的
测地线坐标是 Riemman 同构 or Euclidean 同构
compact <==> compact
双曲极坐标
net structure of
距离 , 方向空间 or 其射影 , 测地线长度 都是 invariant. 是 的 isometry group
远离光锥 地定义 (time,future) 网
. 作为测地线球半径
or 距离空间 和方向空间 的 product net struct
极限方式
- 距离连续
- 方向连续
in , 类时类空基本上是对称的, 所以 space like net 也是类似的
((time,future),(time,future)) 连续 at :=
in 双曲极坐标
二次型拓扑合理性的线索: 通过 张量作为线性映射空间, 继承的张量二次型, 将会成比例于 的 Killing form 二次型
推广到高维, 粗略的直观:
Minkowski 可以分解为 dim 距离空间 和 dim 方向空间 , 让我们来使用它们的乘积拓扑
现在我们需要定义方向空间 的拓扑. 我们可以使用 的 dim 测地线坐标. 我们可以使用测地线坐标的拓扑结构, 它是 type 或 type. 通过维数的归纳, 我们需要定义 的拓扑结构, 再次分解为 dim 径向空间和 dim 方向空间 . 现在 dim 方向空间只是双曲曲线, 它是 Riemann 子流形, meitrc 继承自 的 metric
为了用纯二次形式技术定义测地线, 为起点的测地线是嵌入的 型双曲线, 在 型 dim 空间 span by and
二次流形 的切空间可以定义为正交于径向的 (仿射) 子空间
二次流形 的测地线的定义不需要流形技术, 只需要用测地线 as 截线 of 截面 span by (径向 + 切向) + 嵌入的双曲线 及其测地线长度. Question 是否有好的解释?
type (p. 19 of ref-9)
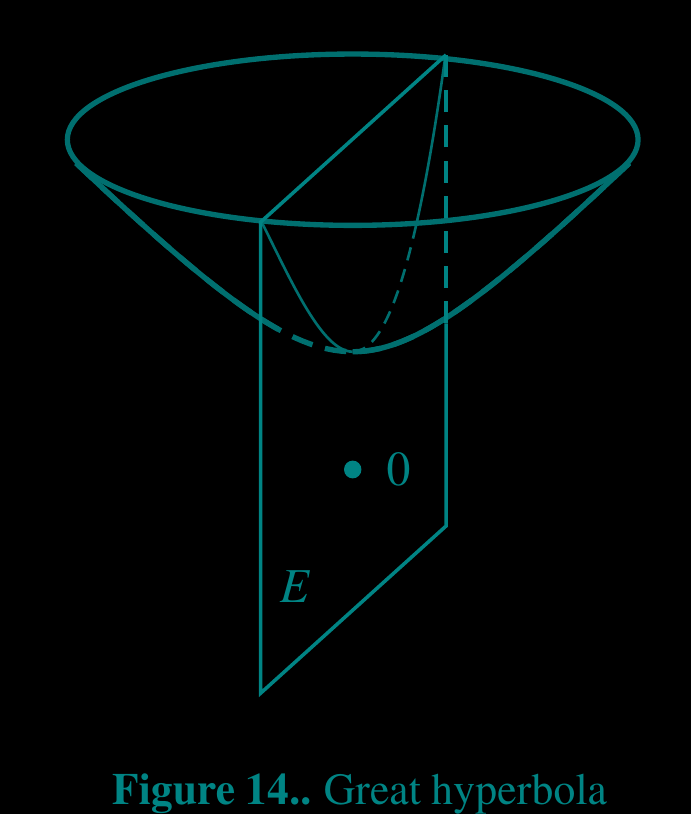
type
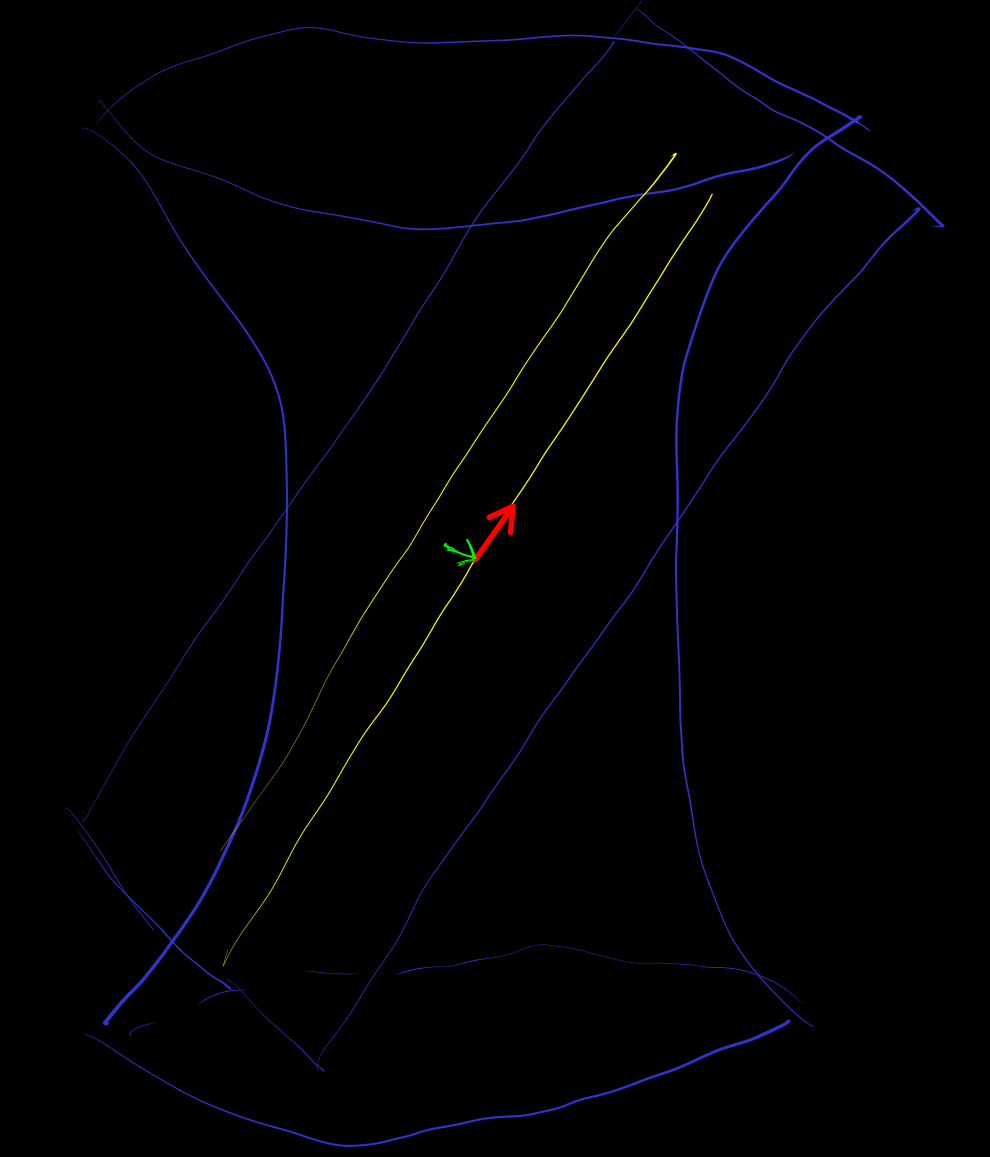
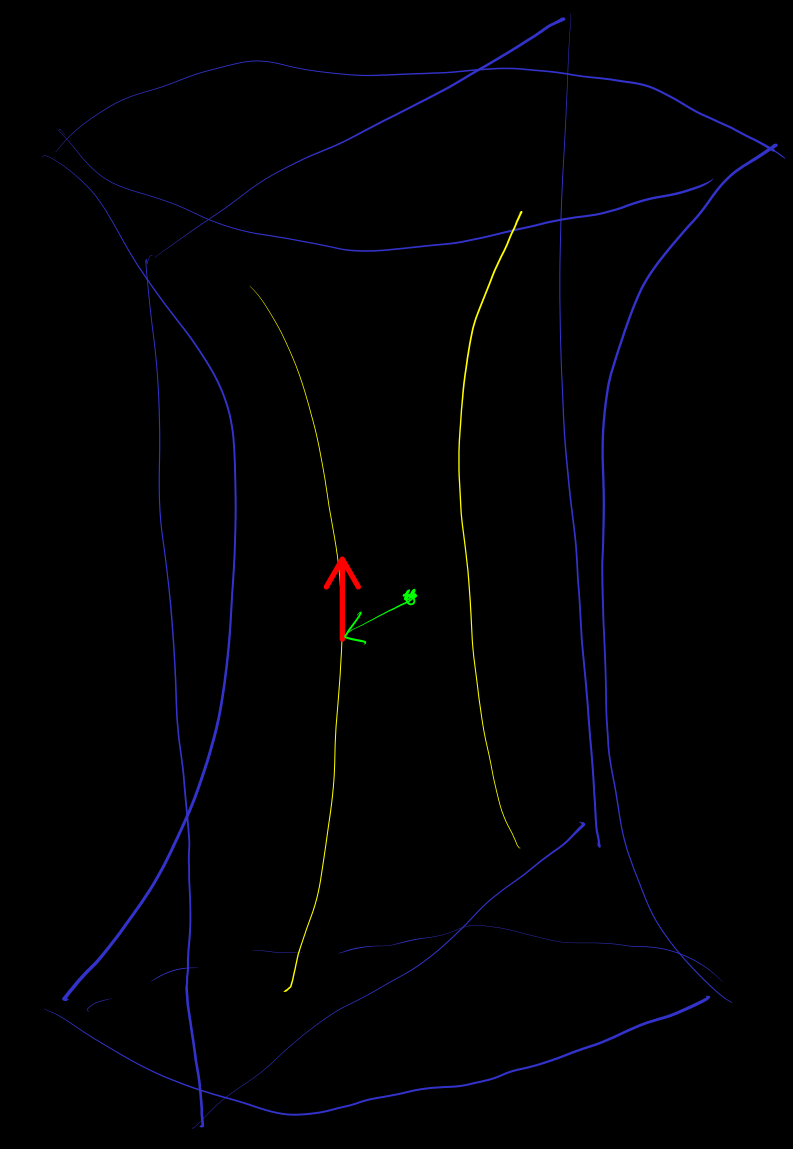
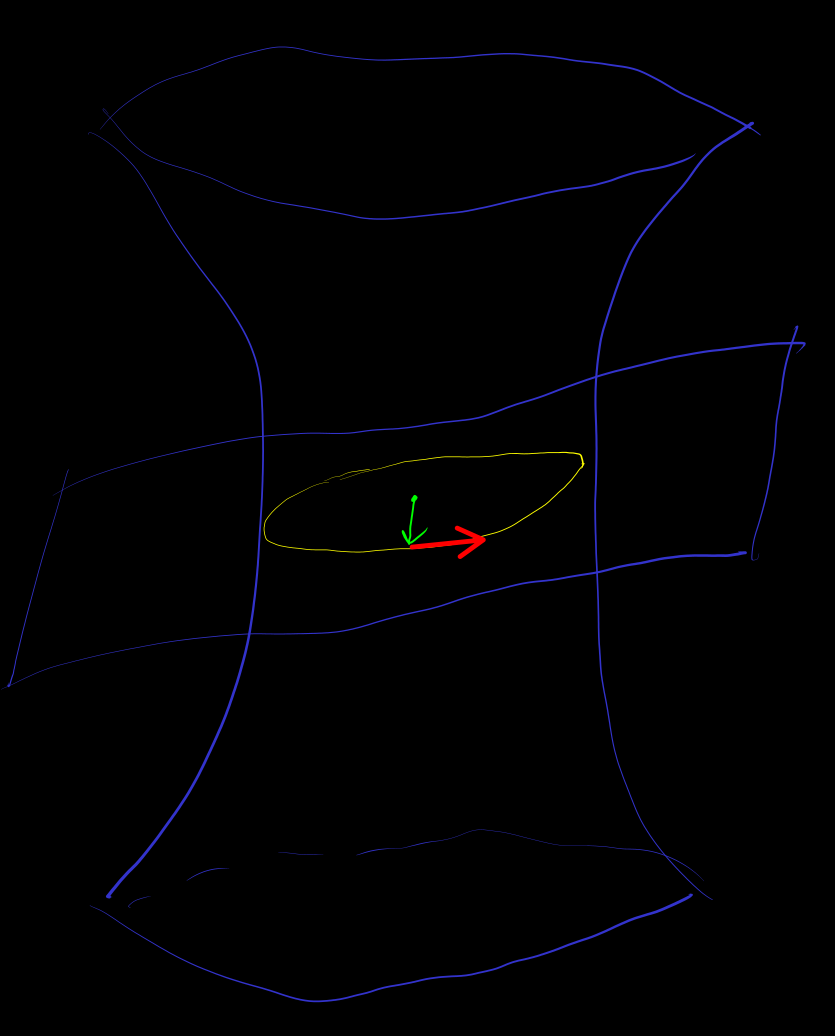
[geodesic-of-quadratic-manifold] 测地线
let
正交补空间 , 维类空
仿射空间 as 切空间 of
let ,
是二维子空间, signature
, 并与 相交得到嵌入的
得到 基点 方向的测地线
测地线球
where
的 (time,future)-like net struct

双曲极坐标 as 距离空间 和方向空间 的 product net struct
极限方式: , . or 距离连续 + 方向连续
(time,future),(time,future) 连续 at :=
in 双曲极坐标 (time,future)
let
正交补空间
仿射空间 as 切空间 of
let ,
- 类时
signature
与 相交得到嵌入的
得到 基点 方向的测地线
- 类空
signature
与 相交得到嵌入的
得到 基点 方向的测地线
不是 Euclidean type metric 流形, 所以测地线球的概念需要修改
space like 方向空间 的测地线坐标 , 根据维数归纳, 使用 的 net struct, 得到 的 local net struct
由于 net 是 product type 分解的, 所以归纳下去大概会分解到多个一维半径, 称之为 [multi-radius-geodesic-ball] . 分解顺序会影响吗?
然后尝试用双曲极坐标 i.e. 距离和方向的 product net struct 定义 的 space-like net struct
然后可以定义 (space,space)-like 连续 at , 或简称 space-like 连续
signature 的情况应该是类似的
的类时网和类空网并不等价
Minkowski 连续定义为 time-like 连续 and space-like 连续
Minkowski 连续同胚定义为 都是 Minkowski 连续
all 都是连续且同胚
一般线性函数可能不 Minkowski 连续
测地线坐标 or 双曲极坐标按照定义是局部 Minkowski 同胚或局部 Euclidean 同胚
是 Riemman manifold, const negative curvature
是 Lorentz manifold, const positive curvature
alias de Sitter space
[hyperbolic-cosine-formula] 双曲余弦公式
let
let
let 未来 time-like.
余弦公式
[isom-top-hyperbolic-Euclidean]
在 距离下的极限结构 测地线距离 Euclidean
Proof
let ,
let
use
use 连续性
推广到 , Euclidean
Proof
use 测地线坐标
similar to , try to prove
where
- 是 的测地线坐标
- 是测地线坐标中的 Euclid 距离
球面 的球极投影的基点在 上. 需要两个以上的坐标卡覆盖全部
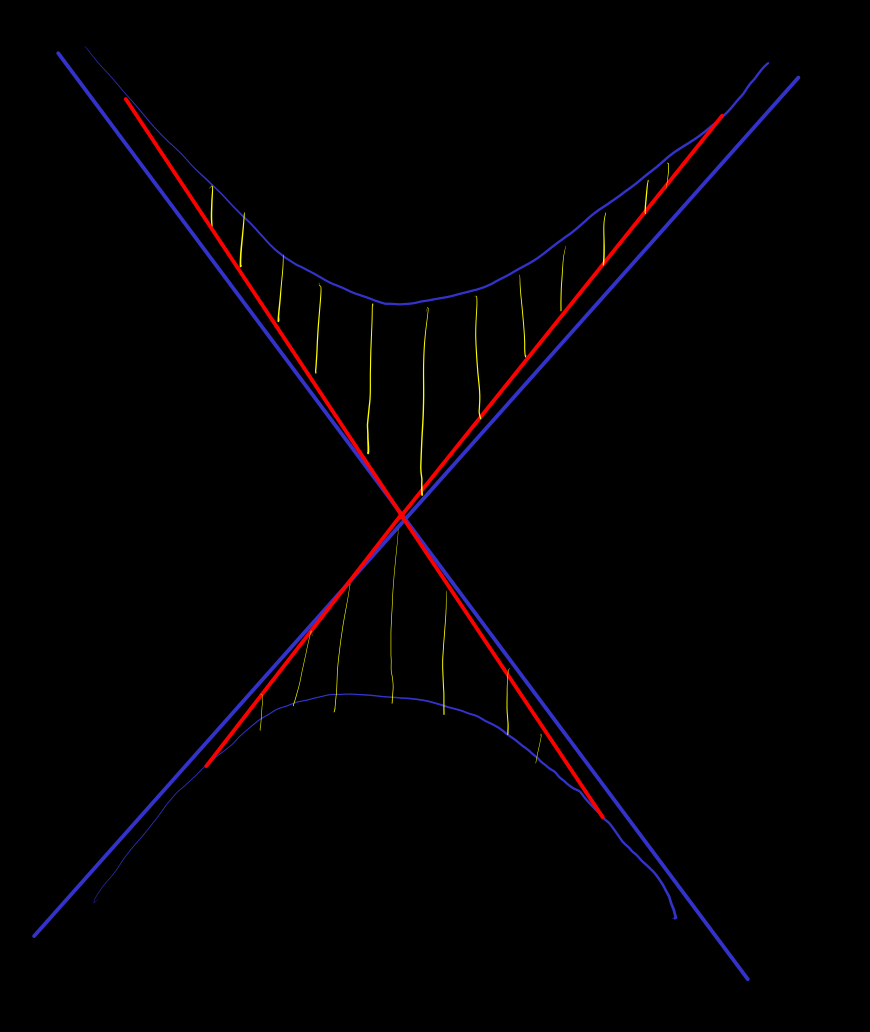
[stereographic-projective-hyperbolic] time-like 双曲面 考虑球极投影, 两个基点分别在两枝双曲面上, 且投影在光锥方向形成分隔的奇点

space-like 双曲面, 用 space-like 基点来定义双曲投影, 而且投影坐标卡是低一维的 Minkowski 空间
转换函数应该是 Minkowski 连续同胚?
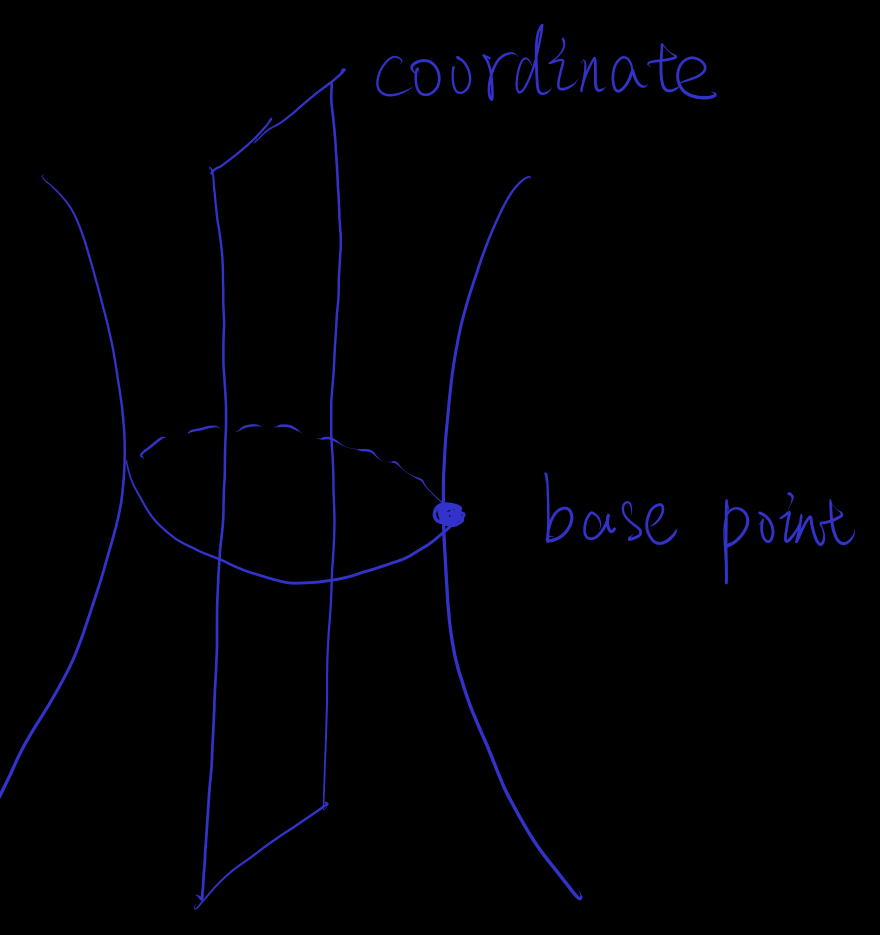
对 的情况进行 3d 作图, 画出基点的光锥 (注意是光锥是 "纵向" 的)
即使画图的直观可能难, 解析计算应该是不难的
可以推广到 and ?