Propositional Logic
Examples of Natural Language
| Proposition | Boolean Value (bool) |
| Humans are organisms | True, true, 1 |
| Iron is an organism | False, false, 0 |
Digital circuits represent bool
| Circuit Value | bool |
| High Level | 1 |
| Low Level | 0 |
I won't deal with the hardware implementation of digital circuits here. I don't know the details either.
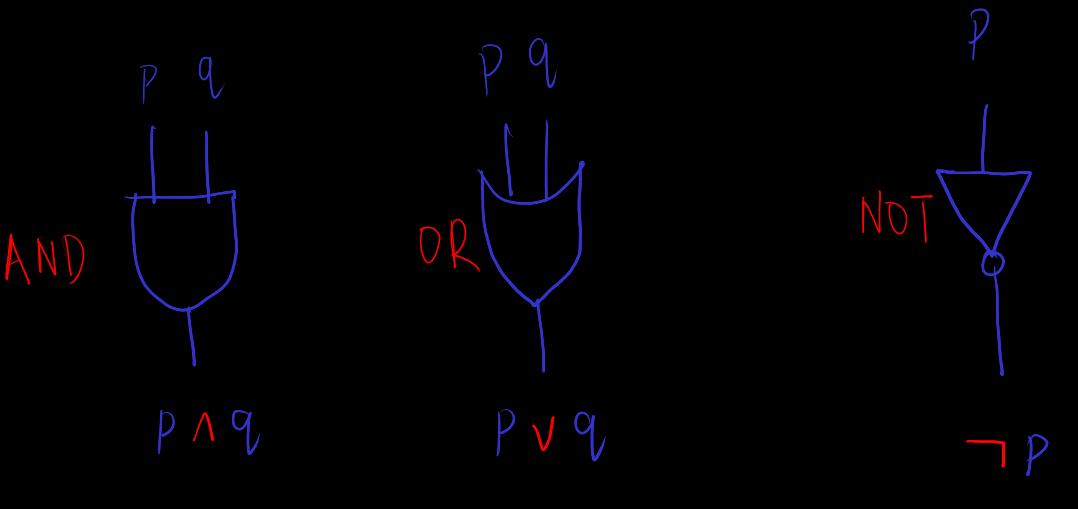
[logic-operator] logical and, or, not
- And,
,
and, logical conjunction - Or,
,
or, logical disjunction - Not,
,
not, logical negation
Examples of Natural Language
| Proposition | Boolean Value |
| Humans are organisms and 1 is a natural number | 1 |
| Humans are organisms and 1 = 2 | 0 |
Formal Language
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 0 |
| 0 | 1 |
Representation of in digital circuits and logic gates
Are gates designed to prevent reverse current?
The not gate converts a low level to a high level, indicating that the hardware implementation of the gate requires external energy and needs to be powered on
"Redundancy" e.g. we can use to represent
Circuit gate implementations start with not,nand or
. But I think maintaining the symmetry of
is useful, cognitively or in terms of negative duals.
[computability] Computability of Circuits
Logic gates can be used to create any function
(image from p.85 of ref-1)

- Construction of input
circuits
require at most
and gates
. Some functions only need a portion of the
inputs, in which case some lines are not connected.
represents the "multiplication" property of value parallel circuits
- Construction of output
In the input, connect the wires that you want to output to 1 to the or gate
Example not xor
Exclusive or,
, xor
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
- Construction of output. Just connect the required wires to or games
If the function does not require complete , the circuit calculation components do not necessarily have to be constructed in this fixed way. It can be further simplified and the use of gates can be reduced depending on the situation. But I won't go into details here
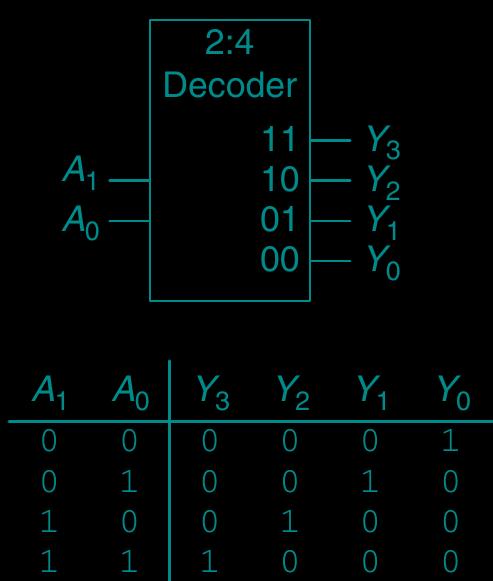
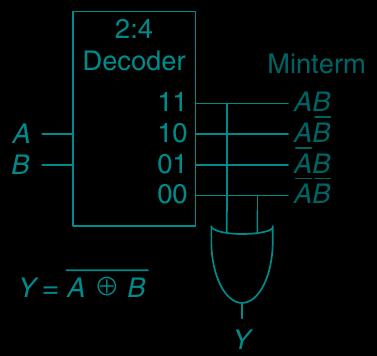
A symbolic representation of multiple input or output lines in a computing unit
[control-circuit] Control circuit, selector or multiplexer (multiplexer)
outputs to , outputs to


inputs require control circuits
[De-Morgan-law] negative dual law or De Morgan's law
Proven by exhaustion, just like how humans count numbers is actually also exhaustion. Same below
[boolean-algebra]
bool algebra is denoted as or
[bool-distributive-law] distributive law
Its negative dual
Inductively ( mean all function )
Similarly
[bool-commutative-law] Commutative law . same for
[bool-associative-law] Associative law . same for
[periodic-circuit] Periodic circuit
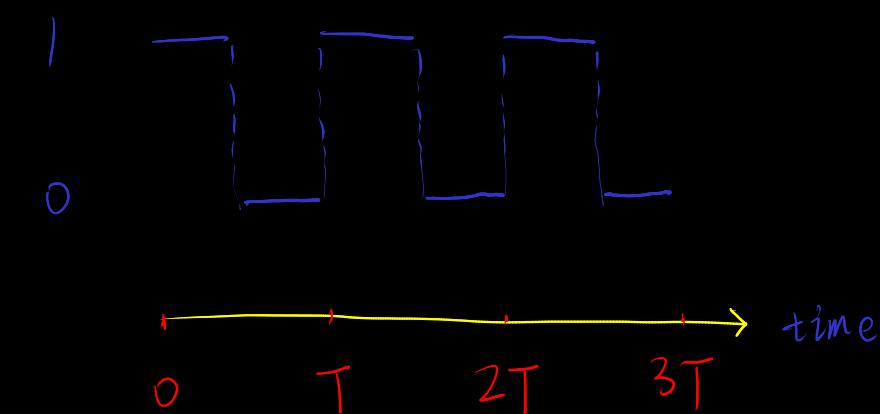
Implemented by crystal oscillator
[memory-circuit] Circuit memory
Black box model
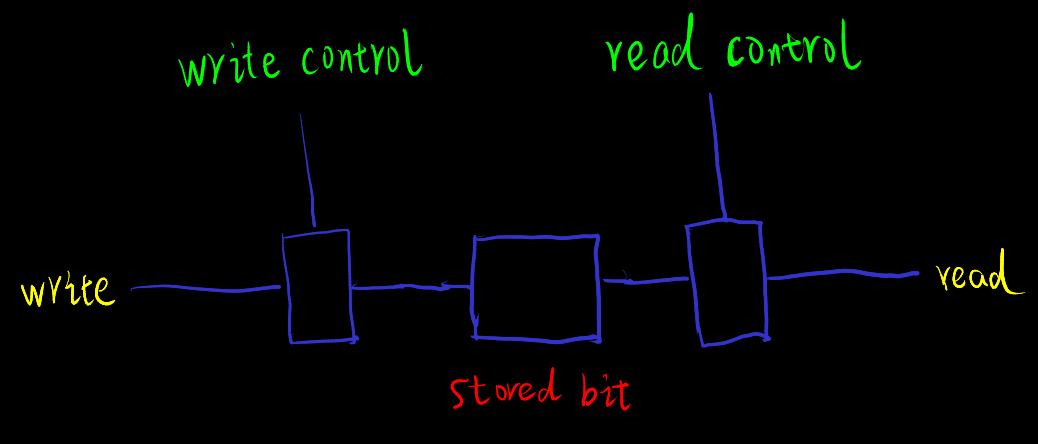
Possible implementation

- Use a ring circuit to reuse the 1/0 value of from the previous cycle
- Inverter (
notgate) ensures current direction and prevents 1 from decaying (through external energy) - In order to write 0 to an existing 1, you need to write 1 to to get , and then invert it to
- Need a higher write voltage than the voltage in the loop to overwrite the previously existing ? e.g. use a higher voltage to overwrite the existing
[finite-machine] Finite State Machine
[i/o] The input of a circuit may come from the outside world (e.g. sensors, keyboards), and the output of the circuit may also reach the outside world (e.g. signal lights, screens)
The rhythm of external input is usually inconsistent with the rhythm of the computer's internal periodic circuit, so the external input needs to pass through synchronization components first
[memory-array] Memory array
Binary, order, natural number. Example is the number of steps from 000, 001, 010 to 111, although this assumes that we can recognize three bits. ,
The range of natural numbers contained in multiple bits, for example, 3 bits of as parameters, to correspond to the real world content. Example Computer's character representation e.g. ASCII, Unicode, the position and color of the light-emitting points on the screen
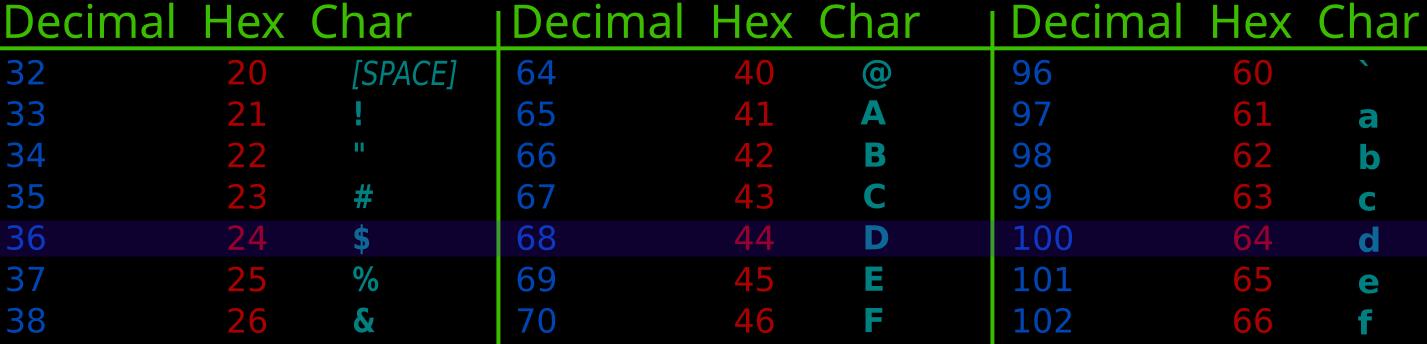
(image modified from wiki media about ASCII)
In practical applications, multiple bits per address are better than 1 bit per address, or a two-dimensional memory array is more efficient than one-dimensional

[instruction] Instruction
Usually represented by multi-bit data written in an address in memory to indicate certain circuit tasks
Some common circuit tasks
- Addition of natural numbers
- Determine whether the bit data meets the required conditions
- Jump to the execution of other instructions
Assume an instruction is completed in one circuit cycle (single-cycle computer)
Example add instruction. add x_1 x_2. The bit data of the instruction is divided into three regions, representing different types of information
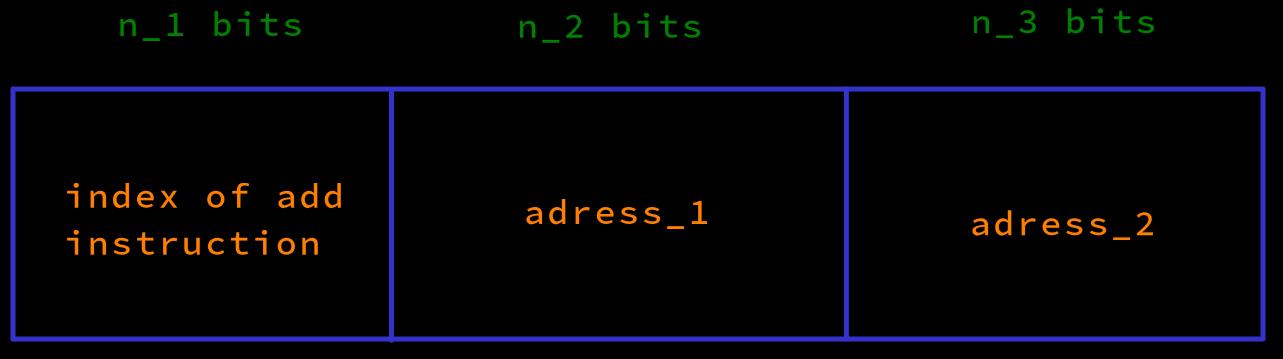
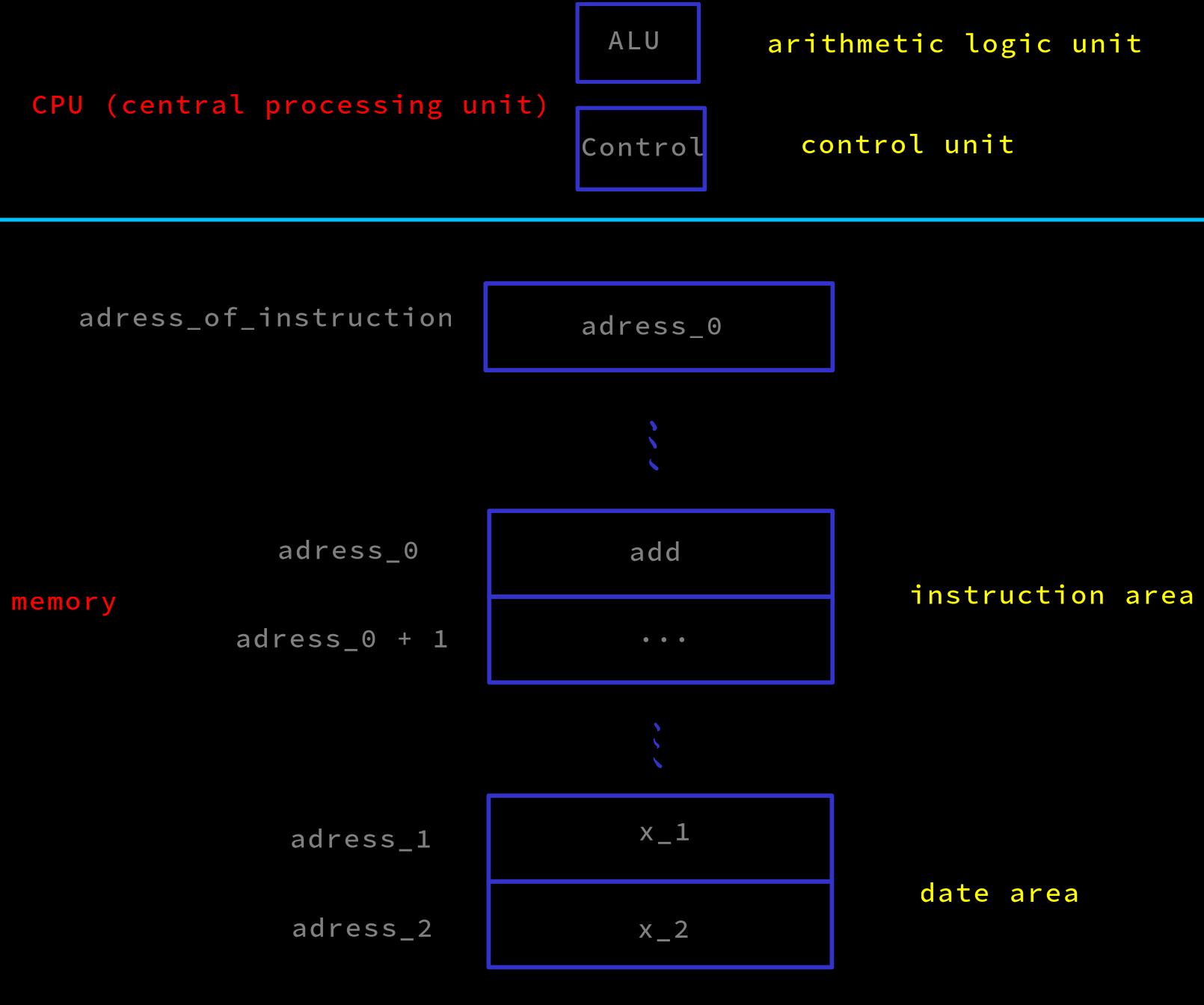
-
Read the
addinstructionaddinstruction atadress_0(add x_1 x_2andadress_1, adress 2are from the source code and compiler generation)- The value
adress_0stored in the fixed memory addressadress_of_instructionis read, the data in the index area of theaddinstruction is sent to the control signal element (control unit), then the control signal is calculated and output (too many details, see ref-1)
-
Execute the
addinstruction- The output control signal is input to the control circuit element of the memory, reading
x_1inadress_1andx_2inadress_2from the memory, and inputting them to the arithmetic element (ALU) - According to the output control signal, the output of the arithmetic element
x_1 + x_2is written toadress_1
- The output control signal is input to the control circuit element of the memory, reading
-
Enter and read the instruction of the next cycle
- The value
adress_0stored inadress_of_instructionis sent to the arithmetic element by a well-designed circuit, calculatingadress_0 + 1i.e. the next instruction address, which is written into the data inadress_of_instruction.adress_0 + 1will be executed in the next circuit cycle
- The value
Other instructions may have more than two data areas (non-instruction index area)
Instruction stream
Example [loop] Loop
The speed of a periodic circuit is far greater than human speed (1 GHz = 10^9 cycles per second)
Loops in high-level programming languages
let i : int = 0;
while (i < 10) {
i = i + 1;
} // result = 10
let i : int = 0;
while (i < 10) {
i = i + 1;
} // result = 10

-
Reading instructions
The
bgt(branch_grater_than) instruction is stored inadress_0. (Instructions are generated from source code and compilers.)10is in one data area ofbgt, while the number of instruction streams3required for the while loop is in another data area ofbgt. -
Executing instructions
Executing the conditional judgment
Read
iand10, compare their sizes in the arithmetic element, give a control signal based on the result, combined with the control signal given by thebgtindex areaPerform different tasks based on the result of the conditional judgment
- When
The arithmetic element outputs a control signal based on this judgment, changing the value stored in
adress_of_instructionto the address of the next instructionadress_0 + 1-
The instruction at
adress_0 + 1is to perform the taskUse the
addinstruction to calculatei + 1and write it back toadress_1 -
After executing
add, we need to return to the judgment of the next loopThe next instruction after the
addinstruction is thejumpinstruction. The result of the execution is to modify the value ofadress_of_instructiontoadress_0, implementing the jump of the instruction and performing the judgment of the next loop
- When
The arithmetic element outputs a control signal based on this judgment, changing the value stored inadress_of_instructiontoadress_0 + 3, breaking out of the while loop, and executing the subsequent instructions
[compile] [parse]
Use a parser to verify the correctness of the token stream language, essentially it's going through all language rules, i.e. enum + match (or if else) + recurse, by programming lang or circuit lang. or using a (generated) finite state machine
The operation of the parser requires generating large and complex data structures in memory (some figurative descriptions: tables, nodes, trees)
If the data stream is source code of a high-level programming language, an instruction stream can also be generated based on this data structure. This is called compilation (compile), but parse and compile are often used interchangeably
If the language rules are very complex, the language rules can be classified and decomposed (multiple times), first traversing the classification, and then traversing the rules within the classification. Example Separate into "syntax check" and "semantics check"
An enlightening example of the concept of abstraction and API: The items around you can be used conveniently without knowing the manufacturing principle because they are designed that way
Computers, in addition to the advantage of high-speed periodic circuits, have other advantages, such as the capacity of memory (1 GB = 2^(30+3) bit = 8589934592 bit) and persistence (power-on time)
They are part of reason why proof assistant are useful for human
Complex data structures and calculation functions can be constructed in memory. It may also be useful for many other fields.
The motivation for variables or variable names is that humans cannot remember so many addresses. Variable names are designed to assist humans with semantics and allow the computer to convert variable names into addresses, based on the variable's position in the overall program logic.
Variables or variable names allow the values stored in memory to be reused through addresses, which can minimize the memory and use of new addresses.