set-theory - note-math

For people, one way to understand natural numbers is counting

For computers (cf. logic.typ), the ways to represent natural numbers are

Periodic circuit
Arithmetic component
Binary
Function that call itself

However, the number of elements in the set of natural numbers is infinite, while bits and computer memory are finite. Human memory is also finite

The problem of infinite space: Reality cannot build circuits and memory with infinite space. Even if it could, it would be limited by the finite speed of electricity.

But potentially infinite time can be used to achieve "potential infinity"

Assuming that the upper limit of memory is infinite but the memory occupied in each cycle is limited, the program has infinite possible inputs, which is also a potential infinite

However, there are even sets with an uncountable number of elements. Example

the set of all subset of ,
all function from to itself,

Verifying the correctness of set theory language requires a parser, memory data structures, and functions. The implementation of the generated computer instruction stream is not the focus of this goal.

Motivation for sets/types

Modularization and multiplicative decomposition to simplify cognition

Example Natural language's Subject-Verb-Object SVO (subject, predicate, object). Suppose there are 10 nouns and 10 verbs. Suppose we "forget the SVO rule", then verifying the grammatical correctness of a three-word sentence requires at most times. If we understand and use the SVO rule, it requires at most times.
If the number of elements in a set is infinite, then the set/type limits the concept, making it possible to say it in a finite amount of time

Complex set theory objects, propositions are stored in variable names, so humans still need to check all the complex definitions stored in variable names, so readability is very important

Parser or proof assistants can allow humans to reduce from reviewing all steps to reviewing definitions (and check all the code logic of compiler), skipping a large number of detailed proof steps, and then determine the correctness of the proof result. This is like the case of APIs

The human brain compiler can omit and supplement omissions, trading temporary efficiency for error-proneness and forgetfulness

Assistance also has other functions, like the case of, Programming before the era of IDE/LSP/friendly-and-interactive-compiler-error-messages/documentation was painful. The organization, structuring and reuse of data and information were not done well, and the powerful capacity and time of memory of computer were not used well.

Example of proof assistant: acornprover, in development.

[proposition] proposition is a special (string, bool) product struct computer data structure. For mathematical language, the string field uses special construction rules to restrict it, and this restricted version of the string is called a formula

Because we cannot directly judge the truth or falsehood of a guess, we need a language with undefined truth values.

from proposition to unknown proposition, its truth value part is modified to (bool, unknow) sum struct

Abbreviation true proposition and proposition are often used interchangeably

Many propositions cannot be automatically derived by computers, and humans need to find possible paths, input them into the computer for verification, or develop more new automated proof methods.

We will assume some initial propositions that do not need to be proven. And assume rules for constructing new propositions using existing propositions.

Abbreviation Use the same symbol for formula and proposition, " is true/false/unknow",

[formula]

let symbol be type of math object, then is a formula

is similar to value : type or variable_name : type in programming language

symbol is not math object

equal

let be object, then is a formula

and, or, not

let be formula, then

is formula

forall, exists

let be formula built with i.e. read in memory, used by some specific function call, then

is formula

inference , equivalent is formula

[equivalent]

Some equivalent uses. For finite computer data, the following calculation results can be exhaustively proven to be equal

Similarly, in order to represent the case of "infinite elements", define language expansion or specify language transformation. For example, De Morgan law of infinite elements

The concept of "infinity" is limited by using the symbol string of declare-element-of-set

formula, proposition is a special data structure in memory. It can be considered that math_object, formula, proposition are the type of programming language

Many propositions are equivalent, so we can consider the "quotient" type of propositions, but the possibility of equivalence is infinite, whether it is possible to have an exhaustive algorithm, first depends on whether it is countable …

Similar to the redundancy of , set theory construction rules may also have redundancy, or there are many equivalent definitions

Specify (finite)

transitive :=

follow various rules of bool in the finite case, define language transformation rules: let is formula built with independent/parallel i.e. independent/parallel in memory read and used by specific cuntion, then

[commutative-forall-exists]

same for

[distributive-forall-exists]

Natural language example of derivation

If it rains, I won't go out
It's raining
So I won't go out

This example is similar to a conditional branch

let rain : bool;

let out : bool;

match (rain) {

  true => out = false,

  false => out = undefined,

};

let rain : bool;

let out : bool;

match (rain) {

  true => out = false,

  false => out = undefined,

};

similar to if block in many programming language, automatically skips the execution area when the condition is not met

if (rain = true) {

  out = false

if (rain = true) {

  out = false

[inference] For mathematical language, that is

The compiler reads the formula
The compiler reads the formula is true proposition (may be custom)
The compiler reads the formula is true proposition
Then the language rule setting is that the compiler, according to this condition (from memory), assigns the bool value of the formula to true i.e. sets is true proposition

[proof] The proof is that compiling passes is true proposition

Although I am confused by this type of vacuous argument like is always true proposition, there is no reason to abandon defining the intersection of local empty set families for a certain set . I can only accept it from a certain perspective, for example, treating it as true without a constructive proof, thus automatically skipping it, or skipping over an if block in a programming language without generating an error …

If this type of vacuous implication is accepted, then

and find that is

[reverse-inference] Reverse inference. If the result is that I went out, then it is definitely not the result of rain. If the result of the conditional branch is out = true, this is not the result of rain = true. Since the bool value of an ideal binary computer must be one of two, it can only be the result of rain = false. This can be written as a conditional branch

match (out) {

  true => rain = false,

  false => rain = undefined,

};

match (out) {

  true => rain = false,

  false => rain = undefined,

};

Mathematically, reverse inference is written as formula , and defined equivalent to

[reverse-proof] Proof by contradiction is that compiling passes is true proposition

Deductive proof also requires syllogism

All living things die
Humans are living things
Therefore, all humans will die

Where "all living things die" is a specially constructed proposition

[syllogism] Syllogistic reasoning is a language rule

The compiler reads the formula is true proposition (possibly from a definition e.g. union))
The compiler reads the declaration let is true proposition
The compiler reads the formula
Then the compiler sets is true proposition according to this condition (from memory)

That is, the compiler implements the specific construction of data (finite) according to the declaration (possibly "infinite")

Or understand it as, this rule and behavior are defining the concept of itself

It is also usually written as the equivalent rule let , then the special inference formula is always true proposition. This form is often used in what previously said, "proving is compiling passes is true proposition"

Reverse syllogism: let , then the equivalent formula is true proposition

We may never know whether a proposition of bool unknow can be constructively proved, i.e. compiled successfully in a limited number of steps

Where does the target proposition come from? It may be related to a model of the real world

The proof requires expanding a large number of sentences, although computers are very fast at processing strings. In any case, performance optimization? Use only when needed (lazy load)? Parallel (parallel) when two propositions are not interdependent? Assume already proven results (incremental compilation)?

A proposition has many proofs with different runtime data flow

The following discusses math-object-construct-rule alias set-theory

From a practical perspective, as long as the underlying logic is equivalent, we should choose the most convenient and easy-to-use ones, no need to strictly follow an existing framework.

[natural-number]

natural number and natural number set is object. is true proposition

However, computers cannot handle infinity. In order for computers to represent the natural number set using a finite number of characters and memory, and the function are treated as finite symbols in memory addresses, and the following is defined as a true proposition:

Is it equivalent to telling the computer how to continuously with an instruction stream? Also related to induction.

The cost of finite characters is potentially infinite time, always relying on counting or periodic circuits.

Definition language expansion

Since "definition language expansion" is long, it is usually abbreviated to "definition" "def"

In fact, the symbol is often used to represent definition language expansion or specified language transformation. The for specific natural numbers can be directly defined as comparing memory values using computer circuits.

[declare-element-of-set]

If is non empty (this information comes from the definition of ), we can define symbol and construct true proposition (let)

Finite declare statements can be constructed.

[product]

let be set, let is set

The data structure meaning of the expression in memory should be clear.

Abbreviation . in finite case, number of elements

[sum]

let be set then is a set

Also known as tagged union

in finite case, number of element

[function]

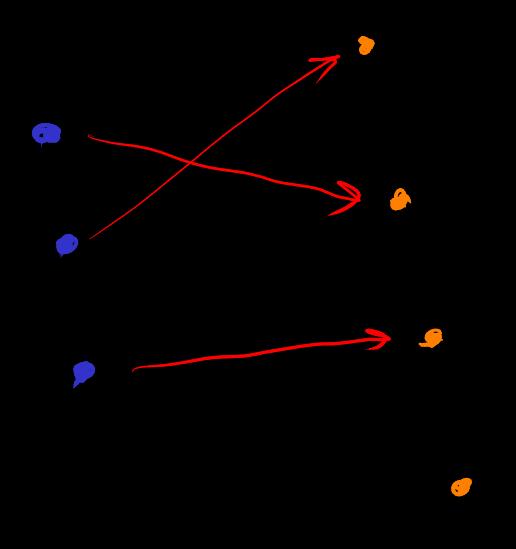
let be set. The rule for defining the function space and mapping as a math object is

denoted by

denoted by . in finite case, number of elements

In a prover, the definition and behavior of a function are: input type + output type + if the same input is checked, the output is specified to be the same.

Prop . Changing to is called normalization of function.

[set-with-element-in-a-type] For type , a set whose element type belongs to is written as , corresponding to the function . The empty set corresponds to the constant false function. The universal set (usually written simply as ) corresponds to the constant true function. Let , define

[simple-set] alias [type]

Sets constructed by the above rules (product, sum, function) are called "simple-set" or "type". Sets constructed by the following slightly more complex rules are general sets.

"An element has only one type" or "no subtypes" is not very meaningful, because we can always add a proposition and use logical and to obtain "subtypes".

In fact, "simple-set" may also use "propositional constraints". For example, the definition of function type, sum type can be the subtype of Product type

For a prover, the language rules of both can be multiplicatively decomposed, also known as "implementing set theory with type theory"

If we choose the simplest thing "type" as the universal set, without any sub-sets or additional constraints, then it's easy to obtain the uniqueness of the universal set.

function space introduces higher-level infinity

One thing that is counter-intuitive at first glance is that we seem to know all or all , but cannot count them cardinal-increase uncountable. But what exactly does "knowing all " mean? In fact, if you try to consider the problem of "finding an infinite subset of in a general way", you will find that it is not simple.

Similarly, although countability can already define some real numbers, e.g. , without the aid of subset or map, countable construction cannot obtain all

The following assumes that sets belong to a certain type

Expand according to type definition

[subset]

Since is false, according to vacuous implication,

denoted by . in finite case, number of elements

let

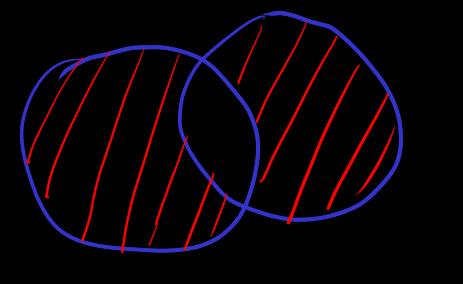
[union]

define object and language expansion

is non-emtpy unless or

[intersection]

According to vacuous implication

[why-type-theory]

Why limit union and intersection to types? Because, since there is no reason not to define the intersection of an empty family of sets and consider it also a set, however, if not limited to types

If no restrictions are placed on the elements in the set , then due to the vacuous argument, the intersection of an empty family of sets results in the universal set , and the universal set is not a set, which violates the construction rules of set theory.
If the elements in the set are restricted to an existing set or (in mainstream set theory) , then the intersection of an empty family of sets produces a local universal set that is or . However, the elements in the set may belong to a smaller or larger set, which causes the universal set to also change, making unstable and without a clear result. This still violates the construction rules of set theory.
In set theory, restricting the intersection of a family of sets to be within the union of that family , has a certain logic to it: it is the minimal common container set for all elements of the sets in . However, this makes the definition of intersection dependent on the definition of union, and this dependency breaks the symmetry

However, every set does have a unique type, thus these problems will be solved.

According to the index mapping , infinite versions of product and sum can be defined.

[product-index]

product component

[sum-index]

sum component

Other uses of

Alias for identifier in memory
Function return value in memory. So should be understood as the return value of the add function is .

[compare-math-lang-with-programming-lang]

What's the difference between ∈ in mathematical language and : in programming language?

Mathematical language and programming languages are very similar, both require a compiler to check a series of language rules.

Some differences:

General practical programming languages already use recursion, but mathematical language treats the recursive instruction itself as a type. Or calls the recursive instruction, as, the recursive definition of natural numbers, or, an instruction to generate natural numbers. This allows us to discuss general natural numbers without generating specific natural numbers (generated by periodic circuits of computers or human brains).
General practical programming languages (without natural number sets and dependent types) only use finite and and or to generate new types, such as struct, enum. This relies on the computer's ability to represent a specific number of natural numbers. On the other hand, mathematical language has infinite versions of and and or to generate new types (or sets), such as forall, exists, which are not represented like finite and or or. And "infinite" can even go beyond countable natural numbers.

At the bottom, mathematical language or programming language both can be represented by periodic circuits, memory bits, and logic gates.

Mathematical language starts with natural numbers (& propositional calculus & set theory rules). For example, real numbers are defined based on natural numbers. However, it still needs the concept of "variables", such as a in let a ∈ A.

General practical programming languages start with built-in types. From a conceptual, cognitive, and application perspective, it is best to regard them as primitive concepts or structures of bits in computer memory, rather than constructing them using mathematical natural numbers.

[hierarchy-order-of-set]

The set constructed above is called a zero (hierarchy) order set, or zero order type

then let be math object, in first order Type

Using object construction rules again, what we get is also defined as belonging to

Anyway, we can always construct such a language with types and bool and various rules in the compiler

let be math object, . And so on …

Example

Can be divided into multiple sentences, so that it is convenient to add/remove properties to get different structs

(Actually is not explicitly necessary, just as the mainstream set theory does not explicitly require )

looks like the set of natural numbers , so should we assume a new hierarchy again? Then for , continue to use the object construct rule … (Will this result in infinite language rule?)

belong to and belong to , but two "belong" have different language rule

language is potentially infinite, and so is hierarchy-order-of-Type language. Of course most of programming language is potentially infinite

Normally we do not need explicit hierarchy of Type. For example, we just need to construct the concrete type like , but not need to mention that the type is a element in type

[universal-type]

The universal-type problem, or the type of every type problem

One thing that's often overlooked here is what the "type" in "type of every type" refers to? What does "type" mean? A binary bool function or a binary predicate logic proposition?

From a constructive perspective, language rules are needed to define a "type". However, to define "type of every type", require knowing all the language rules for constructing "types". Even if we know about logic gates, periodic circuits, and memory, we don't truly know all the language rules or programs unless we actually write them …

Even without considering the "type of every type", self-reference can still arise. In the recursive descent construction rules of mathematical languages, the math_object type does not participate in the construction rules. If a type T self-referentially participates in the construction rules, then the language or program is non-terminal. For example, T : T , even though the memory used in each cycle is limited, the program cannot be completed runing in finite time. Note that, general programming languages also can have infinite loops in program (by different reason)

Suppose a program defines a The concept of universal-type, and universal-type can be used to construct "type", then universal-type self-referentially participates in the construction rules of "type", resulting in a non-terminal language or program

Example [Russell-paradox]

Defined using set theory rules

Then let the compiler calculate the boolean value of the proposition . Since = true, the compiler only calculates the boolean value of , and then finds the not function, so it calculates the boolean value inside not, but this goes back to calculating the boolean value of , and the compiler may choose to enter a circuit dead loop.

For finite sets, , or it is impossible to judge , e.g. , because , or the proposition is not defined as a true proposition.

If we consider the Type hierarchy, for it is very likely that and thus because the first condition does not satisfy

It seems that when we want to use "universal-set" or "universal-type", what we want to use is a higher-order type rule of the current type rule.

Example [self-referential-paradox] "This sentence is false"

this_sentence_is_false : bool = false;

loop {

  match (this_sentence_is_false) {

    false => this_sentence_is_false = true,

    true => this_sentence_is_false = false,

this_sentence_is_false : bool = false;

loop {

  match (this_sentence_is_false) {

    false => this_sentence_is_false = true,

    true => this_sentence_is_false = false,

Or use layering to bypass the self-referential paradox (this_sentence = false) = true. It is considered that they are different sentences and judgments, and that it cannot refer to itself.

[dependent-distributive]

let be set of sets, let , and let be set of sets, index by its elements

union & intersection

sum & product

draft of proof: expand, use parallel distributive cf. distributive-forall-exists

[set-minus]

. if then define

[symmetric-set-minus]