[affine-combination]
Affine combination
is a well-defined affine point, or rather the coordinate definition does not depend on the choice of origin. Let the coordinates of be . Change the origin
Regarding intuition, the simplest example is the proportional point of a straight line between two points
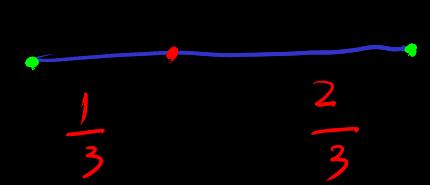
Can be iteratively or decomposed e.g. triangle . And the decomposition operation is commutative. And it can be decomposed into multiple order
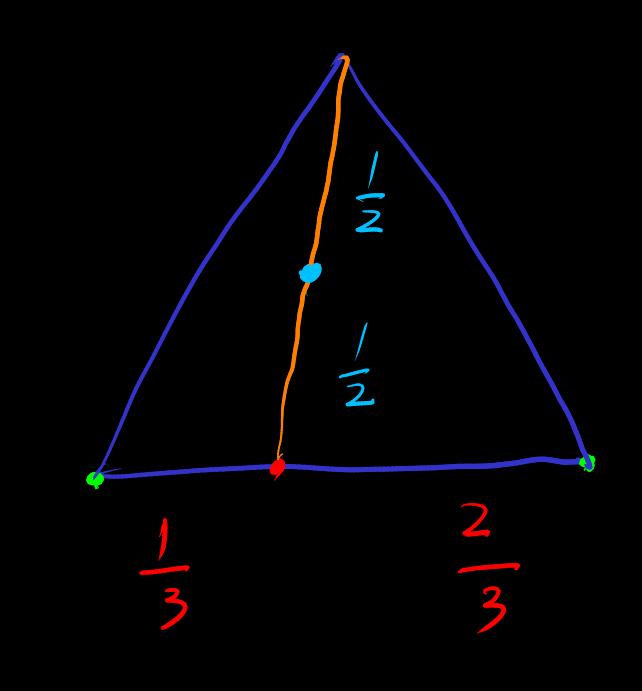
[affine-coordinate] can be considered as a coordinate based on the point . Affine coordinates. alias Barycentric coordinates [barycentric-coordinate]
[affine-independent]
Affine independence := cannot be expressed as
Affine independence corresponds to the linear independence of after selecting one point e.g. as the origin
If it is affine independent, then the vertices correspond to
An -dimensional affine space has at most affine independent points
For the coordinates of affine independent points of an -dimensional affine space , have a one-to-one correspondence with the affine points of
If , although the coordinate will not change due to changing the origin, it is not an affine point
[affine-map-point-ver] alias [simplicial-map] Let be points in another affine space. The affine mapping is determined by , and the situation of other points can be obtained by generating them through affine homomorphism
[center-of-affine-point-set] The center point of is
[convex-hull] := extra
[simplex] := convex hull formed by affinely independent points
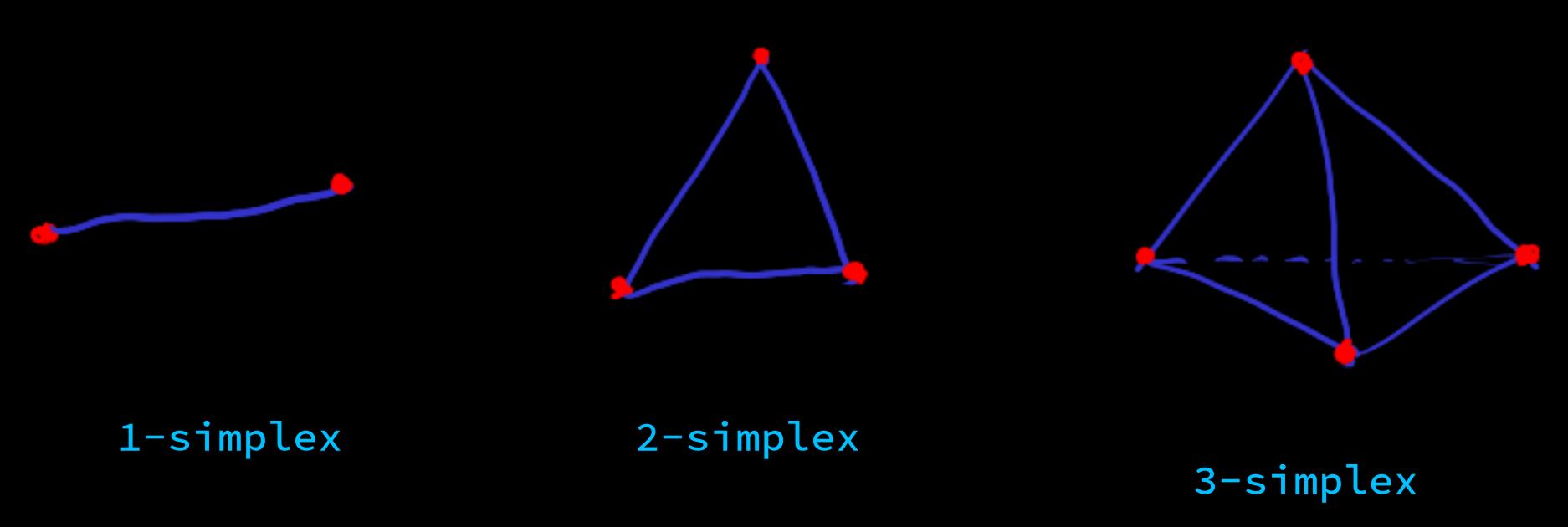
[parallelogram] Due to symmetry, the description of parallelepiped can be simplified from the convex hull of points to the description of points, after selecting the origin
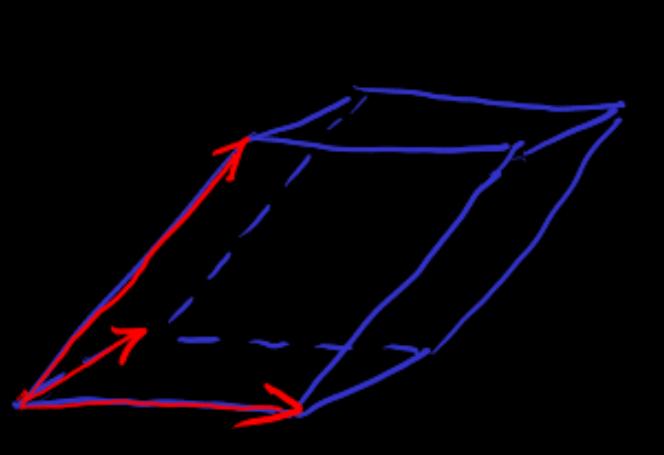
[parallelogram-simplex-correspond]
A parallelepiped can be decomposed into simplexes that are equivalent under translation and reflection
The permutations of points
Corresponding simplex
with
Conversely, a simplex also gives many parallelepipeds with it as one of the simplex blocks
The structural strength given by these two things is about the same
[volume-of-parallelogram] Volume assumption for
- Translation invariant
- Reflection invariant (unsigned volume)
- Finite -> finite volume
- If are not linearly independent, then in the lower-dimensional subspace, so the -order volume is defined as zero
[volume-of-simplex] is of volume-of-parallelogram
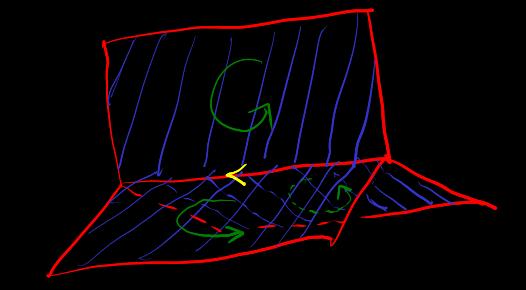
[shear-transformation] After decomposing the parallelepiped into simplexes, cut and translate to form a new parallelepiped with the same volume. Called shear transformation. e.g.
(image from p.587 of ref-3)
Shear transformation volume invariance is algebraically e.g. or
Scaling of edges . e.g.
The stretching and shearing of parallelepipeds corresponds to the decomposition of into elementary linear transformations, which is also used in Gaussian elimination (although they can be used for matrices)
[volume-determinant] The volume change of parallelepiped is
Choose a basis of , the volume of the parallelepiped generated by it is , and the volume of other parallelepipeds is
This is the oriented volume. The set of parallelepipeds remains the same, so the absolute volume remains the same, but the directions of and are opposite
Oriented volume = Unoriented volume + Direction factor
linearly dependent ==> in a lower-dimensional subspace ==> zero volume. At this time, can be extended to , and zero volume algebraically corresponds to
For 's -th order parallelepiped and simplex
Map the parallelepiped to 's -th order alternating tensor 's decomposable element
[try-to-define-volume-of-low-dim] How to define low-dimensional volume? Consider two methods. Similar to linear form vs quadratic form. The first is like defining as or , the second is similar to defining or
- A basis of gives a basis of the alternating tensor space
Use it to define volume: For each , a special alternating multilinear function or form of , defined as , forall
So for a general parallelepiped the volume is
The volume of a nonzero decomposable alternating tensor can be zero, such that . The shear transformation of order does not hold for order
Question A special basis is selected, so what other bases have the same result? or what is the linear subgroup that keeps the volume unchanged?
does not preserve dimensional volume. e.g. or does not preserve dimensional volume
matrix that preserves all order volumes satisfies, for for , , or
Example (sum of elements in the th column). The and cases are similar, i.e. corresponds to the remaining subๅผ
(The cofactor is used in the alternating tensor decomposition representation of , which can be generalized to the alternating tensor decomposition representation or Laplace expansion of )
Example
matrix preserves all volumes satisfies
a coordinate representation of the solution
is an affine line of passing through . or is not its subset
- Select a non-degenerate quadratic form
Derive the quadratic form of the alternating space . Undirected volume or . According to the orthonormal basis and its coefficients , write it as a standard quadratic form
<==> volume is zero
In the non-Euclidean case, light-like will have an impact
Different signature volume definitions will be different for the same set of order
The two volume definitions coincide for
[convex-hull-decomposition] convex hull optimal decomposition to simplex, the method is not unique. Troublesome combinatorial problem
Example
's points
's points. First select simplex, that is, select vertices
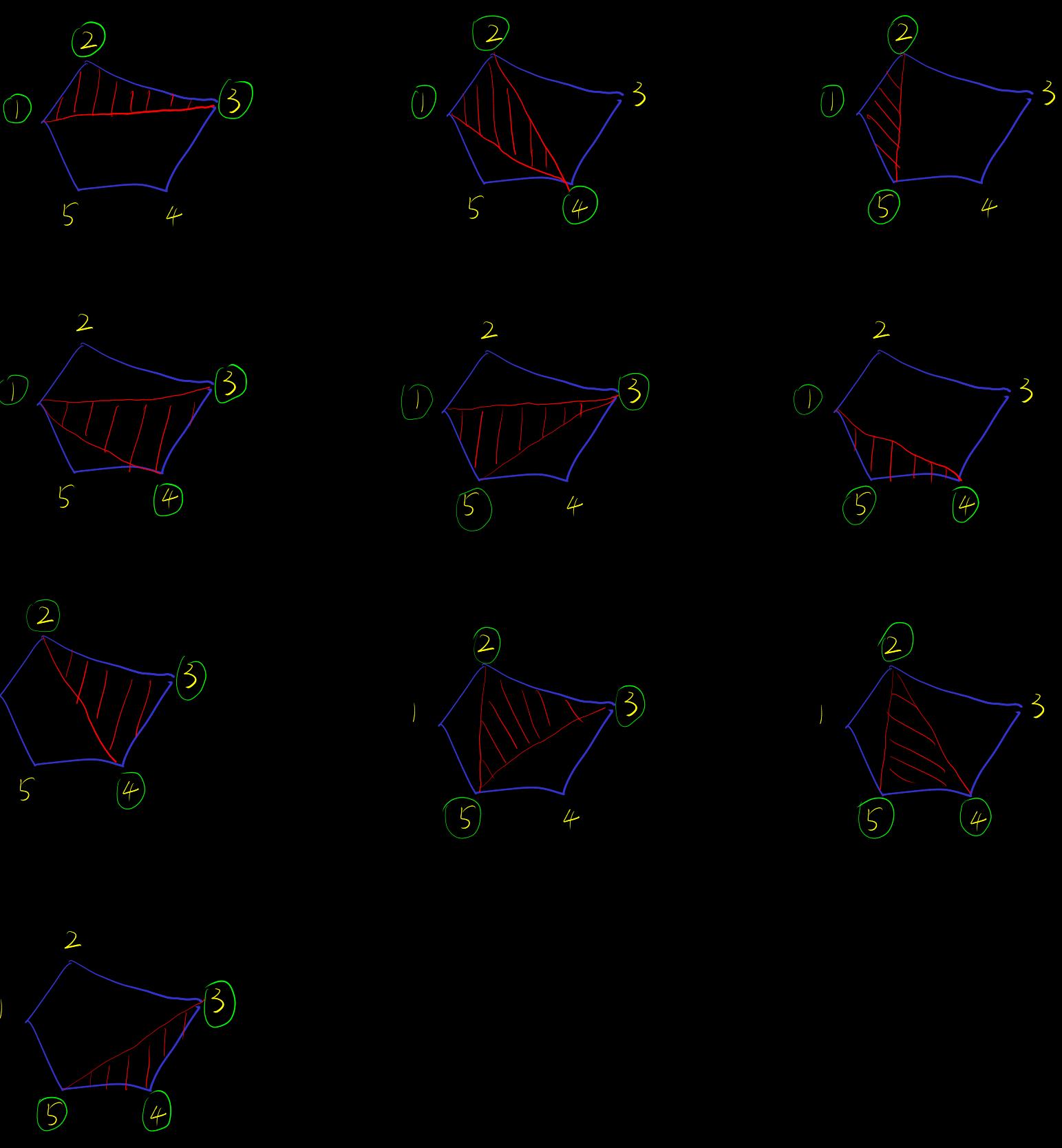
Find out which simplex combinations are decompositions of the convex hull
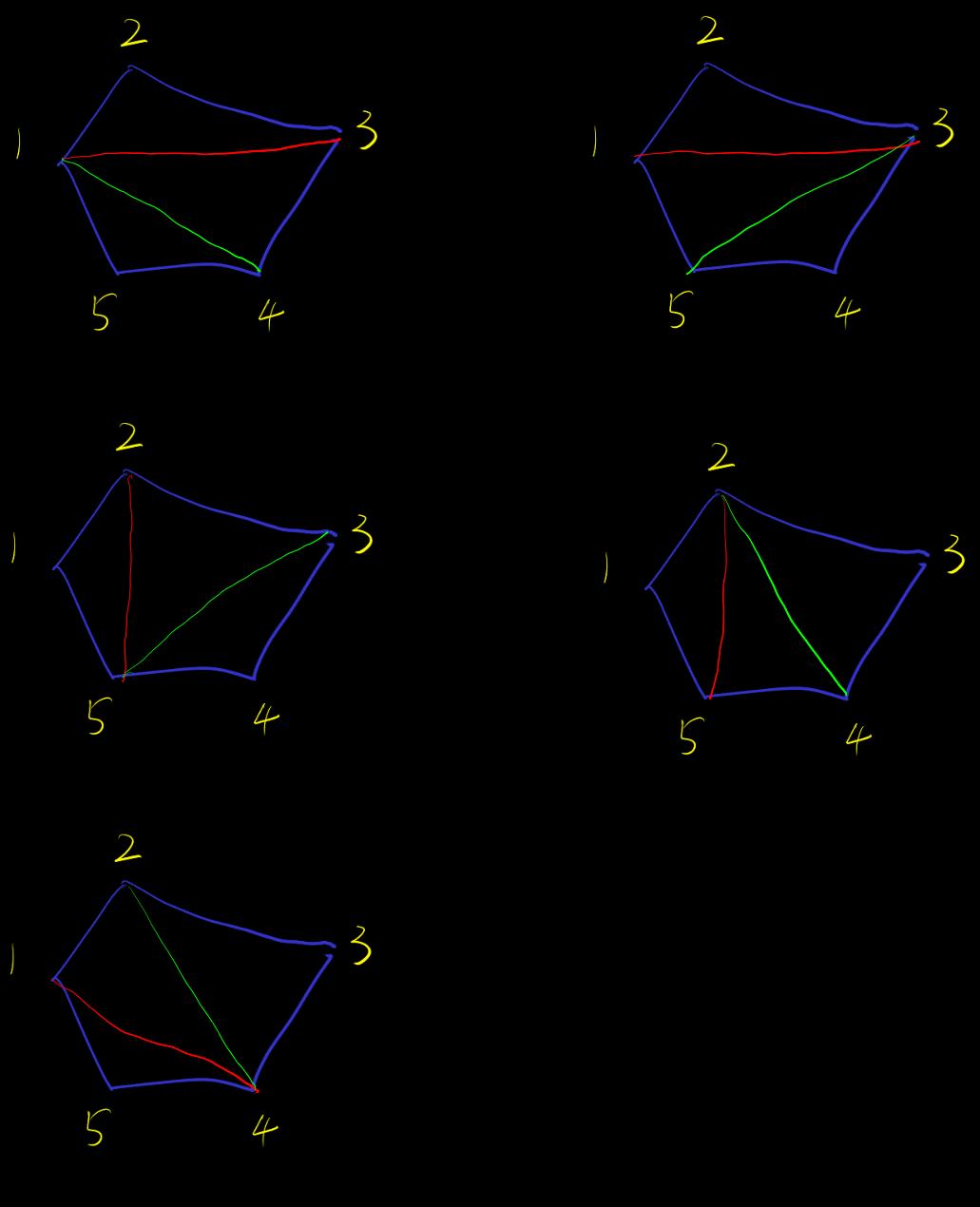
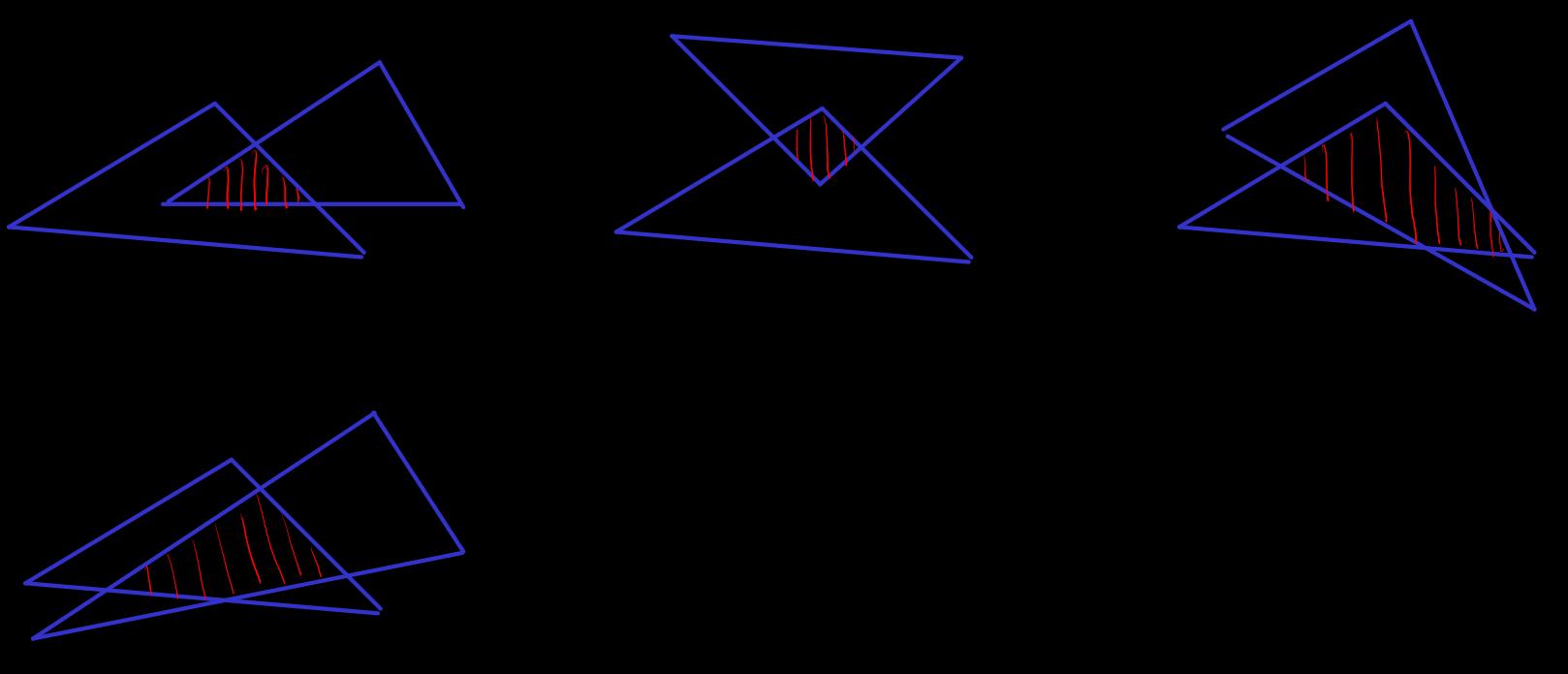
The intersection of convex hulls is a convex hull
Example
The reduced set of a simplex may not be a convex hull. But it can still be decomposed into simplex
Example
[polyhedra] Polyhedron :=
n simplex finite union with
- internally disjoint
- transitively connected between two n simplex
- the transitive boundary is n-1 simplex
The dimension of the transitive boundary is to give the polyhedron the best connectivity
[low-dim-polyhedra] Low-dimensional sub-polyhedra. As a submanifold-like setting? i.e. Adjacent simplexes with boundaries in dimension have only two -> piecewise embedded in . Otherwise, consider the example of a three-connected boundary
Countable generalization -> Countable polyhedron
[polyhedra-measurable]
Polyhedron measurable set . Approximate with a countable polyhedron , symmetric difference cover with countable simplexes as a measure estimate error
Sets define distance (ref-12)
Measurable set :=
Distance from set to "origin" is and
If then
Proof by
Note that such measurable sets have good connectivity. In one dimension, there are only intervals, excluding the SmithโVolterraโCantor set, etc. Operations such as the union of polyhedral measurable sets are also restricted.
[Lebesgue-measurable] If transitive connectivity is not used, then the definition of a general measurable set is obtained. alias: Lebesgue measurable set. Non-measurable sets exist.
[Lebesgue-measure]
The symmetric difference of sets satisfies
Corresponding triangle inequality
Proof
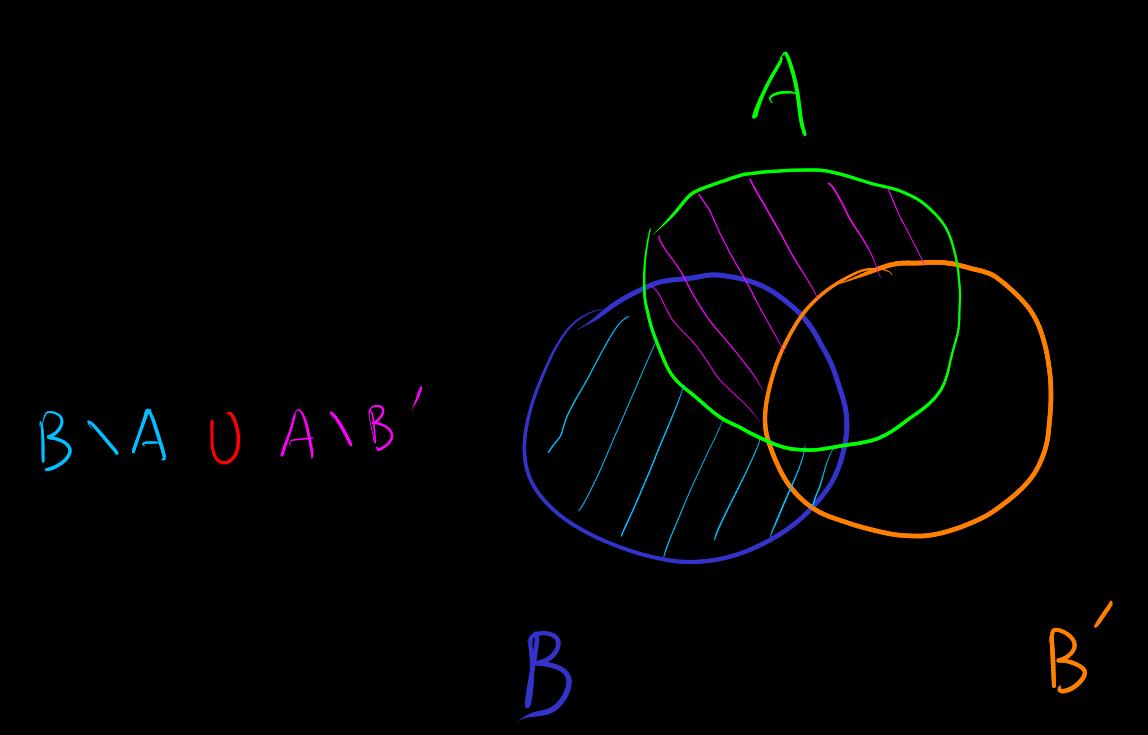
by
The other side is similar
Triangle inequality
For polyhedra with finite volume and
Unique limit
If we use the net of a polyhedron approximating , then there is a limit homomorphism
Obtain the definition of finite measure. The definition of infinite measure comes from the countable approximation of finite measure, or technique
[try-to-define-low-dim-measure] Try to define 's dimensional measurable set. Since the codimension of the region , it is obvious that we cannot use set difference and simplex covering as measure estimation errors to approximate a general " dimensional set"
[pathologic-example-measure-of-boundary]
Using the Euclidean metric structure, some low-dimensional measurable sets can be defined, but there are still pathological examples (temporarily ignore the details, wiki it yourself)
- Painter's paradox. Measure is finite but the measure of the boundary is infinite. Unbounded region is used
- Koch snowflake. The measure is finite, but the measure of the boundary is either undefinable or infinite. Uses a boundary that is nowhere differentiable.
An example of approximating volume but not approximating the boundary volume
- Schwarz Lantern
- Infinite staircase approaching the hypotenuse of a triangle or circle ( ) or as long as there is large normal oscillation,
[measure-theoretic-boundary]
Measure theory boundary. Dimension โ some supremum โ may not be a natural number but a real number
For measurable sets of polyhedra, intuitively, boundary = the maximum minus the minimum in the zero-measure set quotient of the measurable set
For general measurable sets, intuitively, boundary =
where means that the overall scaling of a simplex centered on any goes to zero
or boundary = neither inside nor outside. Inside = limit , outside = limit
Lebesgue differentiation theorem says that the measure of the boundary is zero
- The interval division of the sides of a rectangle gives a rectangular product-style division
- Connecting the center of a simplex to points has ways to divide a simplex into sub simplices
- Or use the midpoint of all lower-dimensional simplices on the boundary
