In order to deal with the power series of , we need to deal with the series of the range first.
For now, only consider the timelike future case.
[sum-preserve-time-future] let be timelike future, then is timelike future
let be timelike future or
then is timelike future or
, or monotonically increasing [increasing-length-of-time-future-series]
let time future, not co-linear. cf. signature-of-2d-subspace-of-spacetime
Through transformation, we can assume that the center of the geodesic ball is
[sum-preserve-angle-range]
let the directions of be contained in the geodesic ball of
==> the direction of is in the geodesic ball
Proof
Question Is there a more direct proof?
let
let
Mapping the geodesic length of the hyperbola to the spatial axis is a monotonically bijective map (Figure) The geodesic length of a hyperbola, , is a bijection. The hyperbola map to the spatial axis and is a bijection. After composition, it is , a bijection, remains monotone.
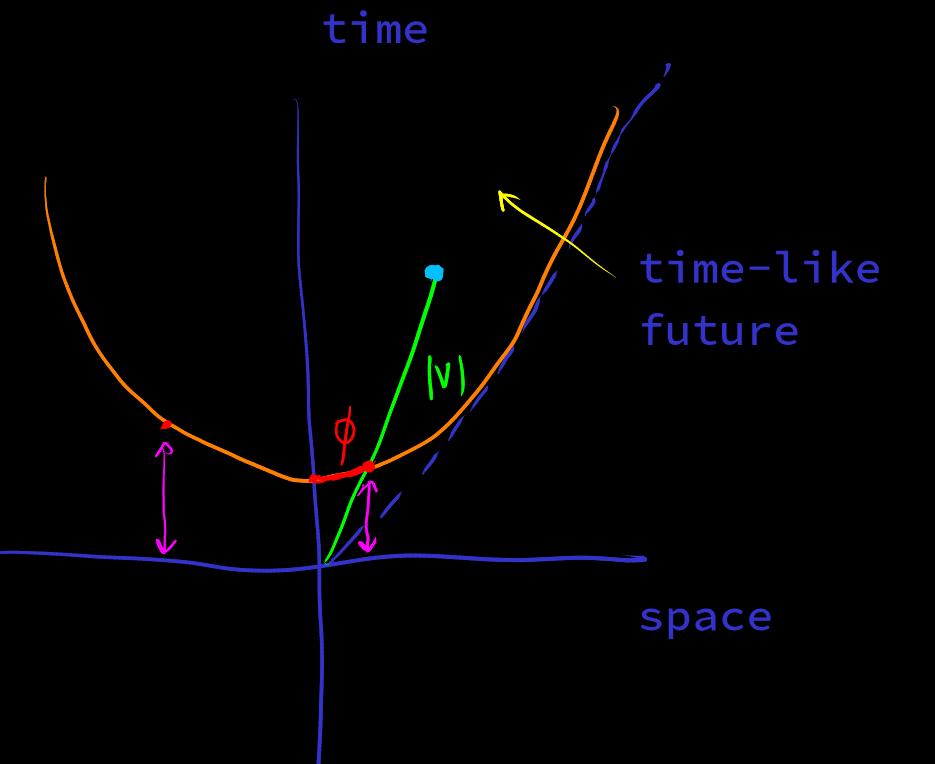
let direction in geodesic ball
==>
Proof use signature , embed , induction
[quadratic-form-inequality-Minkowski-another]
let the directions of in geodesic ball
==>
Proof use cf. hyperbolic-cosine-formula
let time future, direction in geodesic sphere with radius
==> use
[absolute-convergence-Minkowski-distance] ==> monotonically increasing bounded limit exists
[Minkowski-power-series]
let
- Distance limit exists (previous theorem)
- Direction , limit existence to be proved
have property
- time future
Called Minkowski series convergence
Proof of convergence in direction space
- Direction converges
Question Is there a more direct proof
use isom-top-hyperbolic-Euclidean. distance restricted in is equivalent to the geodesic distance as a Riemman manifold, subtraction of two elements is spacelike
we prove Cauchy in
==> is a Cauchy sequence
==> all
, exist
, all
let
. use subtraction of two points is spacelike
use (or other) does not affect the limit
use sum-preserve-time-future. is time-like, . use triangle inequality , use Cauchy
==>
==>
==>
==>
==> Cauchy in
- Inner product converges
let
let
time future
for
use hyperbolic cosine
- is time-like
where
- future
where
Process power series
let
[Minkowski-analytic] Minkowski analytic
(zero order does not affect)
let geodesic coordinates
Target's property
-
time future ==> time future
-
Defining the norm gives absolute convergence
- Question Similar to the Euclidean case, the radius of convergence contains Minkowski continuity i.e. continuity of distance and direction, and has absolute uniform convergence properties
Example Question
-
is Minkowski analytic
-
Similar to complex analysis, analytic ==> Minkowski analytic
-
Similar to the Euclidean case, PDE, characteristic functions, and special functions may provide more examples of Minkowski-analytic
Question let Euclidean analytic , ==> Minkowski analytic?
Question Regarding Minkowski analytic, consider corresponding to Euclidean's analytic-continuation, power-series-space, analytic-space
More , parameter
Series or function triangle inequality may need to add a version with parameter correction
When approximating the net of analytic function spaces, we also need as the limit of the entire direction space