1. notice
  3. 中文
  4. 1. feature
  6. 逻辑
  7. 2. 逻辑
  8. 3. 集合论
  9. 4. 映射
  10. 5. 序
  11. 6. 组合
  13. 微积分
  14. 7. 实数
  15. 8. 数列极限
  16. 9. ℝ^n
  17. 10. Euclidean 空间
  18. 11. Minkowski 空间
  19. 12. 多项式
  20. 13. 解析 (Euclidean)
  21. 14. 解析 (Minkowski)
  22. 15. 解析 struct 的操作
  23. 16. 常微分方程
  24. 17. 体积
  25. 18. 积分
  26. 19. 散度
  27. 20. 网极限
  28. 21. 紧致
  29. 22. 连通
  30. 23. 拓扑 struct 的操作
  31. 24. 指数函数
  32. 25. 角度
  34. 几何
  35. 26. 流形
  36. 27. 度规
  37. 28. 度规的联络
  38. 29. Levi-Civita 导数
  39. 30. 度规的曲率
  40. 31. Einstein 度规
  41. 32. 常截面曲率
  42. 33. simple-symmetric-space
  43. 34. 主丛
  44. 35. 群作用
  45. 36. 球极投影
  46. 37. Hopf 丛
  48. 场论
  49. 38. 非相对论点粒子
  50. 39. 相对论点粒子
  51. 40. 纯量场
  52. 41. 纯量场的守恒流
  53. 42. 非相对论纯量场
  54. 43. 光锥射影
  55. 44. 时空动量的自旋表示
  56. 45. Lorentz 群
  57. 46. 旋量场
  58. 47. 旋量场的守恒流
  59. 48. 电磁场
  60. 49. 张量场的 Laplacian
  61. 50. Einstein 度规
  62. 51. 相互作用
  63. 52. 谐振子量子化
  64. 53. 旋量场杂项
  65. 54. 参考
  67. English
  68. 55. notice
  69. 56. feature
  71. logic-topic
  72. 57. logic
  73. 58. set-theory
  74. 59. map
  75. 60. order
  76. 61. combinatorics
  78. calculus
  79. 62. real-numbers
  80. 63. limit-sequence
  81. 64. ℝ^n
  82. 65. Euclidean-space
  83. 66. Minkowski-space
  84. 67. polynomial
  85. 68. analytic-Euclidean
  86. 69. analytic-Minkowski
  87. 70. analytic-struct-operation
  88. 71. ordinary-differential-equation
  89. 72. volume
  90. 73. integral
  91. 74. divergence
  92. 75. limit-net
  93. 76. compact
  94. 77. connected
  95. 78. topology-struct-operation
  96. 79. exponential
  97. 80. angle
  99. geometry
  100. 81. manifold
  101. 82. metric
  102. 83. metric-connection
  103. 84. geodesic-derivative
  104. 85. curvature-of-metric
  105. 86. Einstein-metric
  106. 87. constant-sectional-curvature
  107. 88. simple-symmetric-space
  108. 89. principal-bundle
  109. 90. group-action
  110. 91. stereographic-projection
  111. 92. Hopf-bundle
  113. field-theory
  114. 93. point-particle-non-relativity
  115. 94. point-particle-relativity
  116. 95. scalar-field
  117. 96. scalar-field-current
  118. 97. scalar-field-non-relativity
  119. 98. projective-lightcone
  120. 99. spacetime-momentum-spinor-representation
  121. 100. Lorentz-group
  122. 101. spinor-field
  123. 102. spinor-field-current
  124. 103. electromagnetic-field
  125. 104. Laplacian-of-tensor-field
  126. 105. Einstein-metric
  127. 106. interaction
  128. 107. harmonic-oscillator-quantization
  129. 108. spinor-field-misc
  130. 109. reference

note-math

幂级数 中的幂函数阶数不同, 引入了系数 的不对称性, 使得不一定适合级数重排? 虽然我们仍然会讨论绝对收敛

一维情况开始

几何级数

in ,

[convergence-radius-1d] 收敛半径

(cf. limsup)

==>

[absolute-convergence-analytic-1d]

==> 绝对收敛

Proof

use 几何级数判别 and

==> 绝对发散

Proof ==> 中无限项

[uniformaly-absolutely-convergence-analytic]

use . use 几何级数控制

in 半径 的闭球 , 一致绝对收敛

多项式函数 是连续函数

收敛半径内, 幂级数定义的函数

,

[analytic-imply-continuous]

==> 连续

将多项式的 change-base-point-polynomial 推广到级数

[change-base-point-analytic]

==> 幂级数 切换基点到 之后的幂级数

在 也有非零收敛半径 . 根据三角不等式,

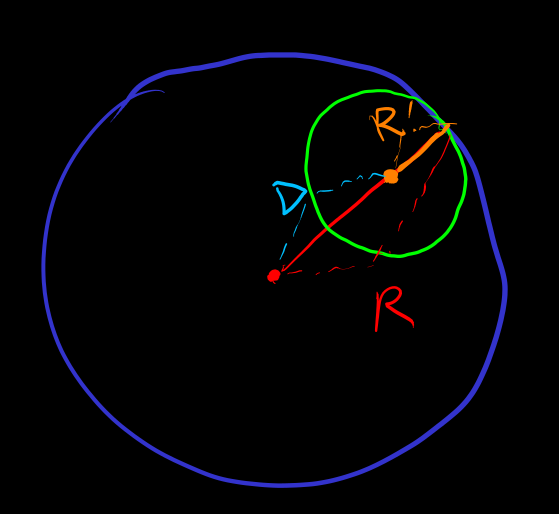
Example

  • 的收敛半径是

  • 的收敛半径是

边界上的收敛问题

  • 的收敛半径是 , 在 处是调和级数 , 绝对发散

  • 的收敛半径是 , 在 绝对收敛到

  • 绝对收敛 vs 收敛: 在 收敛

现在考虑高维的情况. 幂级数

注意 对称性, 例如 的 , 的

将多项式函数 polynomial-function 推广到幂级数

不同于一维, 在高维, 一般没有 . 甚至还没有定义

[linear-map-induced-norm]

let

定义为对所有方向 的一致控制系数. compactness of 将会使得这种定义有意义 (and 无法直接用于一般 二次型方向空间 )

so that (for all direction)

and

和 情况比较, 的定义的可计算性低

[convergence-radius] 收敛半径

[absolute-convergence-analytic]

same as

  • ==> 绝对收敛

  • 存在方向 , forall , 绝对发散

Proof (of 发散)

use linear-map-induced-norm , 存在 使

use 定义, 中无限项

use passing to compact and 子序列收敛到

==> 中无限项

==> 中无限项

将 伸缩到

==>

let

==> 中无限项

另一种观点: 对每个方向 考虑 直线嵌入的收敛半径 . then let

类似一维 also have

  • uniformaly-absolutely-convergence-analytic

  • analytic-imply-continuous

  • change-base-point-analytic

for , 阶 差分 给出

替换

幂级数在收敛半径中一致绝对收敛, 从而可以交换极限

可以恢复 阶单项式

[differential]

阶微分

Example

差分和微分的定义可以用于任何函数, 不需要是由幂级数定义的函数

[polynomial-expansion] 多项式展开

alias 幂级数, Taylor 展开, Taylor 级数

[polynomial-approximation] 多项式逼近

alias Taylor 展开, Taylor 逼近, Taylor 多项式 [Taylor-expansion] [Taylor-approximation] [Taylor-polynomial]

[derivative] 微商 alias 导数, 方向导数

接连的差分和微商

逐次差分 不依赖于顺序 + 极限交换 ==>

[successive-derivative] 逐次微商

==> 幂级数的方向导数表示

逐次微商的概念使用了不同点的切向量的相减, 隐含地用到了 connection 的概念

[partial-derivative] 偏导数

使用坐标. let 是 的基. so 坐标 分量

and so on

let . use successive-derivative, partial-derivative

==> 幂级数的偏导数表示 (also cf. multi-combination)

when domain = ,

define 和对偶基 with

==> 微分的偏导数表示 as 对称张量的 系数–基 展开

when domain =

Example

let

, or

if use range space 坐标 那么一阶微分 表示为 Jacobi 矩阵 [Jacobi-matrix]

[differential-function] 微分函数

将值域 作为 linear space, 使用 power norm, 可以幂级数展开

[successive-differential]

isomorphism

with

same norm

same convergence radius (use )

Proof (draft) 导数的交换性 and . norm estimation

Abbreviation 尽管记号冲突

==> 微分函数的幂级数

[anti-derivative]

  • use

    ==> . 零阶项不确定

  • …

[mean-value-theorem-analytic-1d] 微分中值定理

  • 介值 ver.

  • compact 一致线性控制 ver.

Proof

use reduce to

==> Proof by 介值定理

介值定理使用了完整的 的序

绝对值估计所用的 的序可能没有足够的强度来得到微分中值定理

[fundamental-theorem-of-calculus] 微积分基本定理

微分中值定理 compact 一致线性控制 ver. + compact 分割一致逼近

[mean-value-theorem-analytic] 微分中值定理 for . 用嵌入的直线 reduce to 的情况

  • 一阶

by 微积分基本定理 and chain-rule-1d and

remainder estimation, 一致线性控制

  • 高阶

by 分部积分

remainder estimation, 一致 阶幂控制

let 幂级数

[convergence-domain] 在一点的收敛域 :=

计算幂级数的切换基点后的系数使用了求和的交换

for 多项式, 求和有限, 求和顺序交换, 从而切换基点良定义 change-base-point-polynomial

但是, 无限求和的极限, 如果不是绝对收敛, 并不总是兼容于求和顺序改变 series-rearrangement

幂级数切换基点可能导致收敛域改变

Example

with

收敛域是

切换基点导致收敛域改变

  • , ,

    收敛域 , 半径 的开球

  • ,

    收敛域 , 半径 的开球

不断切换基点可以 "改变" 收敛到的值

Example

let with

let 逐次切换基点 , 最后回到

if 每次位移 都在基点 的收敛域, 并使用幂级数极限

then 最终的幂级数是 , where 是 形成的道路绕 的圈数

  • . 绕 转 圈得到

绕 转 圈得到 , by

[analytic-continuation]

  • 良定义的延拓区域: 不受切换基点的影响

  • 极大延拓区域: 无法再良定义地延拓

Example

  • 收敛半径

不能良定义地延拓到 . by 绕 转 圈得到

极大良延拓区域是

  • 收敛半径

可以良定义地延拓到 , 重合于用 除法定义的

, or

  • 和 已经是极大延拓

的极大延拓是

的幂级数系数包含复数, 不同于 只包含实数

[analytic-function] 解析函数 := 幂级数任何点收敛半径非零 + 极大解析延拓

[analytic-isomorphism] 解析同胚 :=

  • 解析函数
  • same for

Example

  • 是解析同胚

==> , 单调增 ==> 是 解析同胚

, in 有解 ==> ==> 不是 解析同胚

  • with 是 解析同胚
with 是局部解析同胚, 但不是 解析同胚. 非单射:

尝试对幂级数空间定义距离. 启发自

三角不等式 Proof by 两边 power, 二项式展开

[power-series-space]

幂级数空间

网 (note: is linear-map-induced-norm)

(or )

距离

as 一致控制 for forall

幂级数空间是 distance 空间 and complete. Proof by 继承自 of forall

不是 norm, eg.

收敛半径的接近

==>

==>

==>

==>

==>

收敛的值的接近

[Sobolev-space] for Sobolev anayltic space, try use 几乎处处解析 + 作为控制函数去逼近目标函数 , where 是 的 [weak-differential] . (note: is linear-map-induced-norm) 或者只用带解析型积分 norm 限制的几乎处处解析空间, 或者对此空间进行积分 norm 的 Cauchy 网完备化

更弱的网控制

let

use data and new data

Example 包括 的截断多项式逼近, i.e. Taylor 多项式 by

至于解析函数空间的拓扑, 直观是, 逐点用幂级数之间的距离, 然后全局定义域用类似连续函数空间所使用的 compact-open topology 技术

出于对称性的考虑, 解析的定义应该不依赖于特定的幂级数展开基点

不同基点的幂级数距离控制对比

对基点 , 幂级数 with

同时切换基点到

系数估计

==>

关于 递减

==>

let

==>

继续, 有限次

let

==> 一点 的幂级数距离一致地控制区域 的幂级数距离

虽然这仍然无法保持解析延拓的良定义, e.g.

[analytic-space]

解析空间的网

let 解析, with domain

的 网

  • let

  • let and compact and 传递连通, i.e. for , 存在构造 连接

  • forall 解析 with property
    收敛域包含 ,

网的逼近方式: and

when 验证网的性质 " "

if 分离, 需要构造传递连通的 包含

一种可能的构造方式: compact 折线连接 , 使 的有界球覆盖道路每一点, use 有限覆盖

幂级数空间和解析空间处理 阶微分系数

阶微分系数基本没影响

一个基点的 系数的修改同时作用于其他基点, 且不影响 系数,

compare 解析空间的网 vs 连续函数空间的网 (should be something compact open topology?)

in 解析空间及其网

  • [inverse-op-continous-in-analytic-space] ==>

  • [compose-op-continous-in-analytic-space] and ==>

或者说, 算子都是解析空间的连续函数

same for linear , multiplication , inversion ?

Example

  • 仿射线性

收敛半径

任何基点的幂级数的一阶项都是 const

仿射线性空间内能定义一致距离

  • 多项式映射

收敛半径

多项式函数空间内无法定义一致距离

[connected-analytic] in 解析空间, 和 在不同的连通分支?

连通分支内奇点的性质在解析同胚下不变

[homotopy-analytic] 解析 同伦

[power-series-analytic-equivalent] 解析等价的幂级数 := 两个幂级数来自同一个解析函数在不同点的幂级数展开

[power-series-analytic-homotopy-equivalent] 解析同伦等价的幂级数 := 两个幂级数来自同一个解析函数同伦类在不同点的幂级数展开

然后可以幂级数之间的定义不等价版本的性质