Subspace
The following are equivalent
- not co-linear
if , possible
-
2 time(-like)
Example, where
Can linearly generate - 1 time, 1 space
Example - 1 time, 1 null
Example - 2 null
Example . Note that . signature - 2 space.
Example
, where - other cases (symmetry of time space)
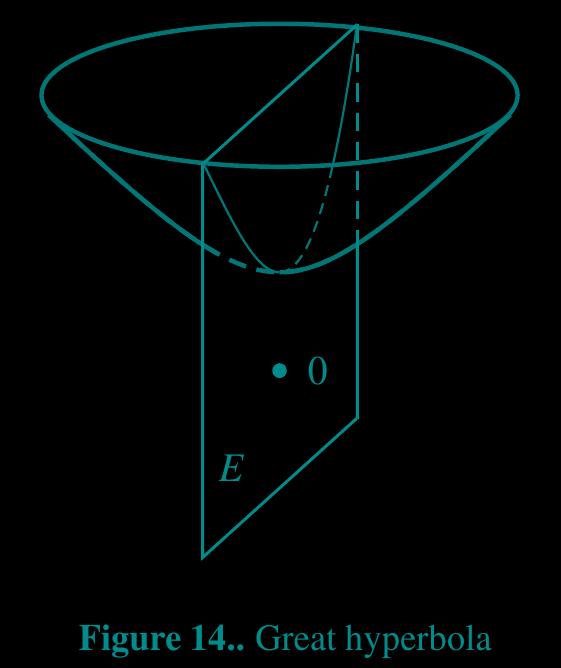
Consider the general in
[signature-of-2d-subspace-of-spacetime] Prop The possible signature of Minkowski in 's is
Prop time-like is only orthogonal to space-like
let time-like. Using orthogonal decomposition, let then ==> space-like
Prop light-like is not orthogonal to
- time-like
- light-like other than collinear with itself [metric-cannot-distinguish-colinear-light-like]
Take an orthogonal decomposition according to the situation
- time-like ==> let ==>
- light-like
We prove that
but
space-like but length zero, so
==>
Prop The signature of the two-dimensional subspace of cannot be or
Proof Use the previous theorem
Prop The signature of expanded by two non-collinear time-like is
Proof Generate an orthogonal basis of with one of them as the initial basis, but the signature cannot be , so it can only be
The projection of is
Prop let , let time-like or light-like with non-collinear. Then
Proof
Known
On the light cone, it is equivalent to solving the quadratic equation for the variable :
Prop The signature of the span of two non-collinear light-like in is or
Proof Euclidean has no light-like, so there is no other possibility
Example
- 's
- 's . Subtracting gives an orthogonal basis
[simultaneity-relativity] Simultaneity in relativity
use orthogonal basis continuation
in , the orthogonal complement of a space-like subspace is a time-like subspace
-
( space-like <==> there exists a time-like that is simultaneously orthogonal to )
-
( not space-like <==> there does not exist a time-like that is simultaneously orthogonal to space-like )
Intuition: Different space-like subspaces cannot be calculated using compatible time calculation methods or the time-like orthogonal complements of are not the same
use orthogonal decomposition
Categorical discussion of . The sign of the product of time components of the inner product determines the sign of the inner product
Categorical discussion of . The sign of the product of space components of the inner product determines the sign of the inner product
in Euclidean, we have inner product inequality ==> triangle inequality
in signature quadratic form, this is generally not true
Derive the quadratic form derived to alternating second-order linear
[quadratic-form-inequality-Minkowski] Inner product inequality
in , let not co-linear, so
quadratic form restricted to , signature
- ==> ==>
- ==> ==>
Proof
==>
quadratic form derived to
signature
-
of ==> of
Proof
of orthogonal basis , ==> orthogonal basis ,==> , i.e. inner product inequality
-
of ==> of
==>
[triangel-inequality-Minkowski] Triangle inequality
- 2 time
,
- ==>
- ==>
- 1 time, 1 null
==>
- ==>
- ==>
Proof of 2 time-like
==>
==>
is uncertain
Example let . let past time-like
Euclidean space can already discuss different convergence directions e.g. whether the sequence converges to . Spiral-like things do not converge in direction space
Euclidean space converges to a point in all directions <==> converges to a point uniformly in all directions, by compactness of
Minkowski space direction space is non compact. Although we have not yet defined the net of
The net of Minkowski space needs to be sufficiently far from the light cone
let
For convergent timelike directions, they can be separated
- Future:
- Past:
- Mixed: quotient away the two leaves , becoming a projective space type direction space
in
let
[hyperbolic-complex] Hyperbolic complex number. cf. split-complex-number
- expand according to the distributive law
[hyperbolic-exp]
use binomial
-
-
-
, . by
[polor-coordinate-hyperbolic]
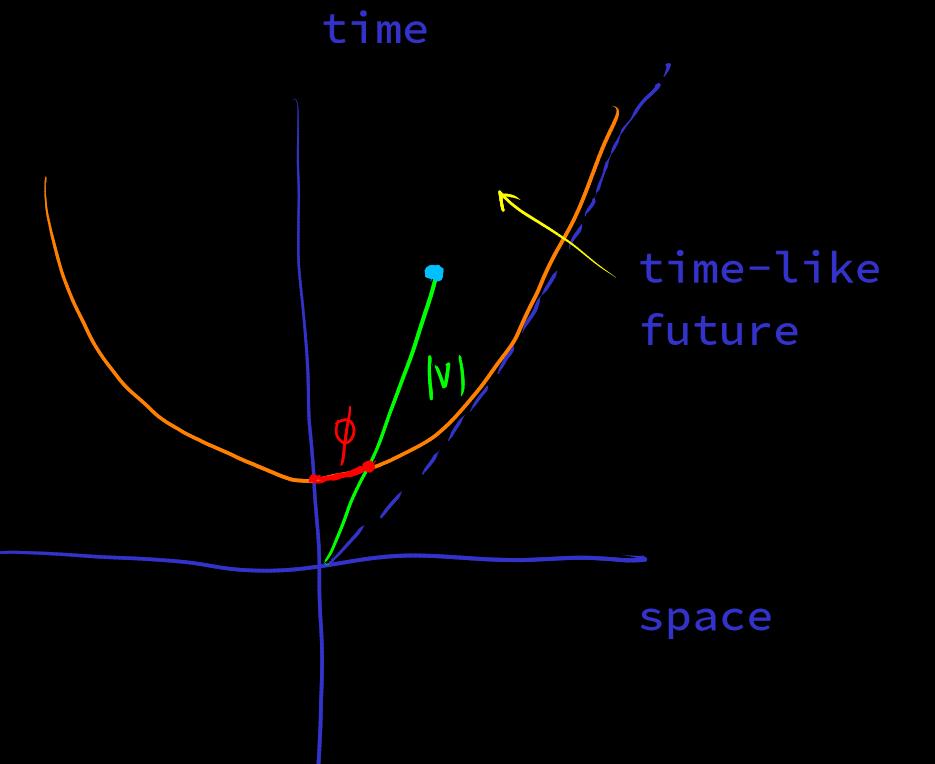
Hyperbolic polar coordinates , , . can come from geodesic length parameter. Also known as hyperbolic angle [hyperbolic-angle]
Polar coordinates are the decomposition of distance and direction
is not the geodesic length of , but the length of
[hyperbolic-isom]
group isomorphism (compare with the case of complex numbers)
monotonically increasing
Solving the quadratic equation yields the inverse mapping
inverse
Question Similar to how uses stereographic projection and , uses hyperbolic projection and to handle hyperbolic angles or geodesic length mapping
The geodesic coordinates of are
Notation conflict. Geodesic coordinates are also usually denoted as , but not defined using algebra
Geodesic coordinates are Riemman isomorphic or Euclidean isomorphic
compact <==> compact
Hyperbolic polar coordinates
net structure of
Distance , direction space or its projection , geodesic length are all invariant. is the isometry group of
Define (time,future) net far away from the light cone
. as the geodesic sphere radius
or product net struct of distance space and direction space
Limit method
- distance continuous
- direction continuous
in , time-like and space-like are basically symmetric, so space like net is similar
((time,future),(time,future)) continuous at :=
in hyperbolic polar coordinates
Generalization to higher dimensions, rough intuition:
Minkowski can be decomposed into a dim distance space and an dim direction space . Let's use their product topology.
Now we need to define the topology of the direction space . We can use the dim geodesic coordinates of . We can use the topology of geodesic coordinates, which is of type or type. By induction on dimension, we need to define the topology of , which again decomposes into a dim radial space and a dim direction space . Now the dim direction space is just a hyperbolic curve, which is a Riemann submanifold, metric inherited from the metric of .
To define geodesics using pure quadratic form techniques, a geodesic starting from is an embedded type hyperbola, in type dim space spanned by and .
The tangent space of the quadratic manifold can be defined as the (affine) subspace orthogonal to the radial direction
The definition of geodesics of the quadric surface does not require manifold techniques, only use geodesic as secant line of the cross-section span by (radial + tangent) + embedded and its geodesic length. Question Is there a better and more intuitive definition?
type
type
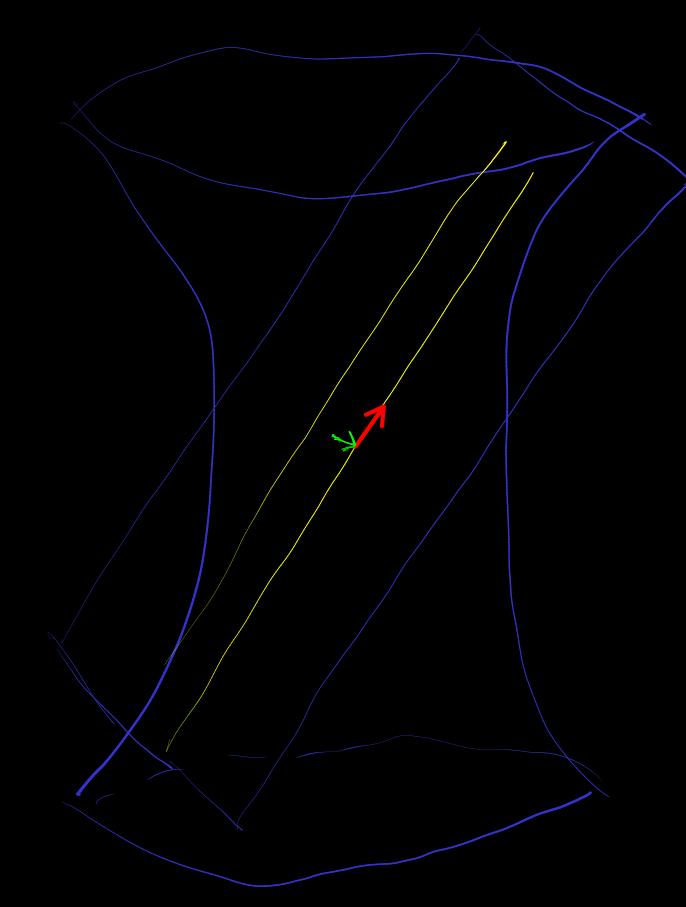
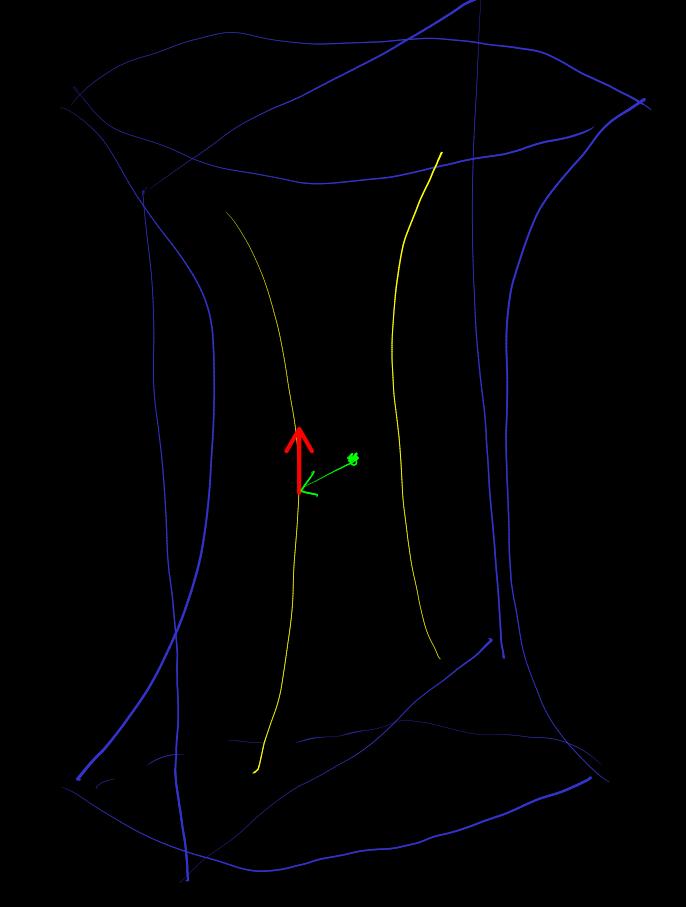
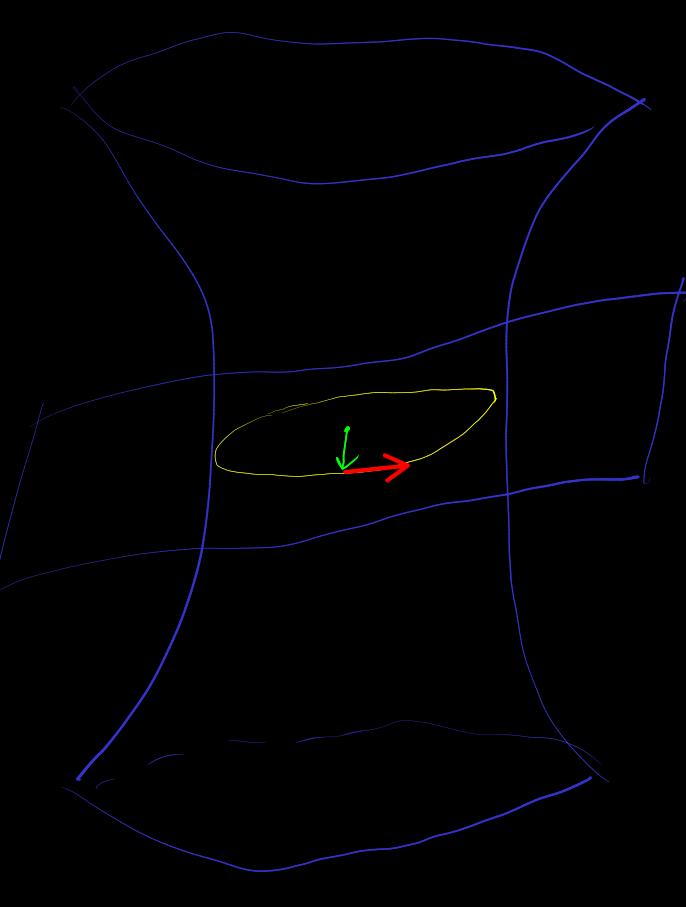
[geodesic-of-quadratic-manifold] geodesic
let
Orthogonal complement space , dimensional spacelike
Affine space as tangent space of
let ,
is a two-dimensional subspace, signature
, intersecting with to get an embedded
Obtain the geodesic of base point in the direction
geodesic sphere
where
(time,future)-like net struct of


Hyperbolic polar coordinates as the product net struct of distance space and direction space
Limit method: , . or distance continuous + direction continuous
(time,future),(time,future) continuous at :=
in hyperbolic polar coordinates (time,future)
let
Orthogonal complement space
Affine space as tangent space of
let ,
- timelike
signature
intersects with to obtain an embedded
Obtain the geodesic line with base point and direction
- spacelike
signature
intersects with to obtain an embedded
Obtain the geodesic line with base point and direction
is not a Euclidean type metric manifold, so the concept of geodesic ball needs to be modified
spacelike direction space 's geodesic coordinates , based on dimension induction, using 's net struct, obtain 's local net struct
Since the net is a product type decomposition, it will probably decompose into multiple one-dimensional radii as we induct, which is called [multi-radius-geodesic-ball] . Will the order of decomposition affect it?
Then try to define the space-like net struct of using hyperbolic polar coordinates i.e. the product net struct of distance and direction
Then we can define (space,space)-like continuous at , or simply spacelike continuous
The case of signature should be similar
The timelike net and spacelike net of are not equivalent
Minkowski continuity is defined as timelike continuous and spacelike continuous
Minkowski homeomorphic is defined as are both Minkowski continuous
all are continuous and homeomorphic
General linear functions may not be Minkowski continuous
Geodesic coordinates or hyperbolic polar coordinates are locally Minkowski homeomorphic or locally Euclidean homeomorphic by definition
is a Riemman manifold, const negative curvature
is a Lorentz manifold, const positive curvature
alias de Sitter space
[hyperbolic-cosine-formula] Hyperbolic cosine formula
let
let
let future time-like.
Cosine formula
[isom-top-hyperbolic-Euclidean]
in limit structure under distance geodesic distance Euclidean
Proof
let ,
let
use
use continuity
Generalize to , Euclidean
Proof
use geodesic coordinates
similar to , try to prove
where
- are geodesic coordinates of
- is the Euclid distance in geodesic coordinates
The base point of the stereographic projection of the sphere is on . More than two coordinate charts are needed to cover all of
[stereographic-projective-hyperbolic] time-like hyperboloid considers stereographic projection, with two base points on the two branches of the hyperboloid respectively, and the projection forms separate singular points in the direction of the light cone

space-like hyperboloid, use space-like base points to define hyperbolic projection, and the projection coordinate chart is a lower-dimensional Minkowski space
Should the transformation function be a Minkowski continuous homeomorphism?
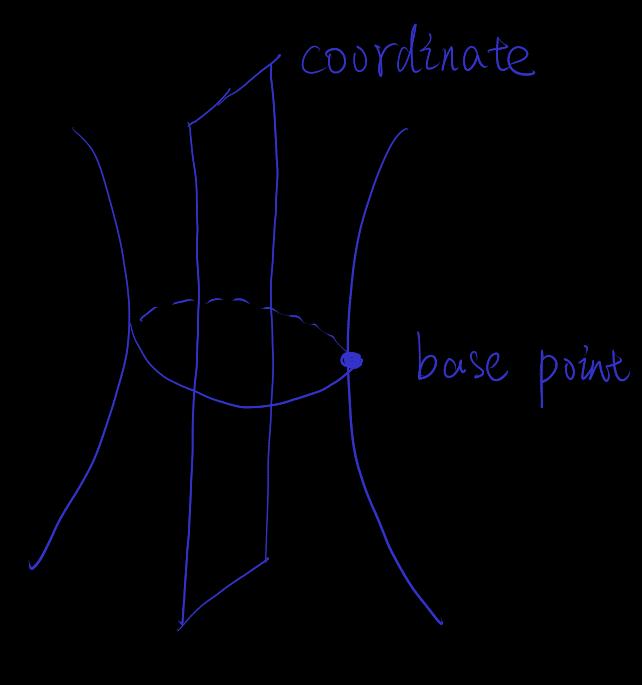
Perform 3d plotting for the case of , and draw the light cone of the base point (note that the light cone is "vertical")
Even if the intuition of drawing may be difficult, the analytical calculation should not be difficult
can be generalized to and ?