The power function order in the power series is different, introducing the asymmetry of the coefficient , which makes it not necessarily suitable for series rearrangement? Although we will still discuss absolute convergence
One-dimensional case begins
in ,
[convergence-radius-1d] Radius of convergence
[absolute-convergence-analytic-1d]
==> absolutely converges
Proof
use geometric series test and
==> absolutely diverges
Proof ==> for infinite terms in ,
[uniformaly-absolutely-convergence-analytic]
use . use geometric series control
in the closed ball with radius , uniformly absolutely converges
Polynomial function is a continuous function
Function defined by power series within the radius of convergence
,
[analytic-imply-continuous]
==> continuous
Extending the change-base-point-polynomial of polynomials to series
[change-base-point-analytic]
==> The power series after switching the base point of the power series to
There is also a non-zero radius of convergence at . (Figure) According to the triangle inequality,
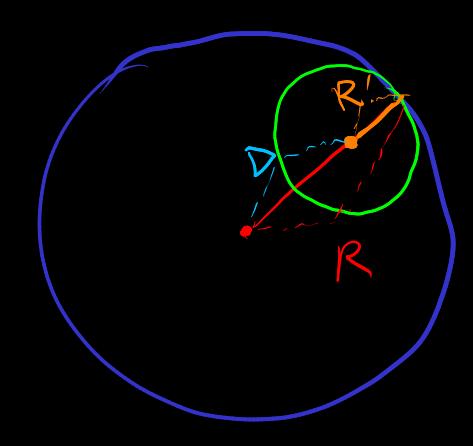
Example
-
radius of convergence is
-
radius of convergence is
Convergence problem on the boundary
-
的 radius of convergence is , at it is the harmonic series , absolutely divergent
-
的 radius of convergence is , at absolutely converges to
-
-
Absolute convergence vs convergence: converges at
Now consider the higher-dimensional case. power series
Note the symmetry, for example of , of
Generalize the polynomial function polynomial-function to the power series
Unlike one-dimensional, in higher dimensions, generally there is no . There isn't even a definition for
[linear-map-induced-norm]
let
is defined as the uniform control coefficient for all directions . compactness of will make this definition meaningful (and cannot be directly used for general quadratic form direction space )
so that (for all direction)
and
Compared to the case, the computability of the definition of is low
[convergence-radius] radius of convergence
[absolute-convergence-analytic]
-
==> absolutely converges
-
There exists a direction , forall , is absolutely divergent
Proof (of divergence)
use linear-map-induced-norm , there exists such that
use definition, for infinitely many terms ,
use passing to compact and the subsequence of converges to
==> for infinitely many terms ,
==> for infinitely many terms ,
Scale to
==>
let
==> for infinitely many terms ,
Another point of view: for each direction , consider the radius of convergence of the line embedding. then let
Similar to one-dimensional case also have
for , the -th order difference gives
Replace
The power series converges uniformly and absolutely within the radius of convergence, so the limit can be exchanged
can recover the -th order monomial
[differential]
th order differential
Example
The definition of difference and differential can be used for any function, it does not need to be a function defined by power series
[polynomial-expansion] Polynomial expansion
alias power series, Taylor expansion, Taylor series
[polynomial-approximation] Polynomial approximation
alias Taylor expansion, Taylor approximation, Taylor polynomial
[derivative] difference quotient alias derivative, directional derivative
Successive difference and difference quotient
Successive difference does not depend on the order + limit exchange ==>
[successive-derivative] Successive difference quotient
==> Directional derivative representation of power series
The concept of successive difference quotient uses the subtraction of tangent vectors at different points, implicitly using the concept of connection
[partial-derivative] Partial derivative
Use coordinates. let be the basis of . so coordinate component
and so on
let . use successive-derivative, partial-derivative
==> Partial derivative representation of power series (also cf. multi-combination)
when domain = ,
define and dual basis with
==> The partial derivative representation of the differential as coefficients of a symmetric tensor – base expansion
when domain =
Example
let
, or
if use range space coordinates then the first-order differential is represented as the Jacobi matrix [Jacobi-matrix]
[differential-function] Differential function
Taking the range as a linear space, and using the power norm, it can be expanded as a power series
[successive-differential]
Proof (draft) Commutativity of derivatives and . norm estimation
Abbreviation Although the notation conflicts
==> Power series of the differential function
[anti-derivative]
-
use
==> . The zero-order term is uncertain
-
…
[mean-value-theorem-analytic-1d] Differential mean value theorem
-
Intermediate value ver.
-
compact uniform linear control ver.
Proof
use reduce to
==> Proof by intermediate value theorem
The intermediate value theorem uses the complete order of
The order of used in the absolute value estimate may not have enough strength to obtain the mean value theorem of derivatives
[fundamental-theorem-of-calculus] Fundamental Theorem of Calculus
Mean Value Theorem compact uniform linear control ver. + compact partition uniform approximation
[mean-value-theorem-analytic] Mean Value Theorem for . Reduce to the case of using the embedded line
- First order
by Fundamental Theorem of Calculus and chain-rule-1d and
remainder estimation, uniform linear control
- Higher order
by integration by parts
remainder estimation, uniform order power control
let power series
[convergence-domain] domain of convergence at one point :=
Calculating the coefficients after switching the base point of the power series uses the exchange of summation
for polynomials, the summation is finite, the order of summation is exchanged, so switching the base point is well-defined change-base-point-polynomial
However, the limit of infinite summation, if not absolutely convergent, is not always compatible with changing the order of summation series-rearrangement
Switching the base point of a power series may change the domain of convergence
Example
with
The domain of convergence is
Switching the base point causes the domain of convergence to change
-
, ,
domain of convergence , open ball of radius
-
,
domain of convergence , open ball of radius
Continuously switching the base point can "change" the value to which it converges
Example
let with
let successively switch base points , and finally return to
if each displacement is within the domain of convergence of the base point , and the power series limit is used
then the final power series is , where is the number of turns the path formed by makes around
-
. Rotating turns around yields
-
[analytic-continuation]
-
Well-defined continuation region: not affected by switching base points
-
Maximal continuation region: cannot be well-definedly continued anymore
Example
- radius of convergence
Cannot be well-definedly continued to . by rotating turns around yields
The maximal well-defined continuation region is
- radius of convergence
Can be well-definedly continued to , coinciding with defined by division
, or
- and are already maximal continuations
The maximal continuation of is
The power series coefficients of contain complex numbers, unlike which only contains real numbers
[analytic-function] Analytic function := Power series with non-zero radius of convergence at any point + maximal analytic continuation
[analytic-isomorphism] Analytic isomorphism :=
- Analytic function
- same for
Example
-
is an analytic isomorphism
-
==> , monotonically increasing ==> is analytic isomorphism
, in has solutions ==> ==> is not analytic isomorphism
- with is analytic isomorphism
Attempt to define distance on the power series space. Inspired by
Triangle inequality Proof by both sides power, binomial expansion
[power-series-space]
Power series space
net (note: is linear-map-induced-norm)
(or )
Distance
as uniform control for forall
Power series space is a distance space and complete. Proof by inheriting from of forall
is not a norm, eg.
The closeness of the radius of convergence
==>
==>
==>
==>
==>
The closeness of the converged values
[Sobolev-space] for Sobolev anayltic space, try use almost-everywhere analytic + as the control function to approximate the objective function , where is the [weak-differential] of . (note: is linear-map-induced-norm) Or just use the almost-everywhere analytic space with analytic integral norm restrictions, or perform Cauchy net completion of this space with integral norm
Weaker net control
let
use data and new data
Example including the truncated polynomial approximation of , i.e. Taylor polynomial by
As for the topology of analytic-space, the intuition is, pointwise use distance of power-series, then for global domain, use compact-open topology technique that similar to what topology of continuous function space use
For symmetry considerations, the definition of analytic should not depend on the specific power series expansion base point
Comparison of power series distance control at different base points
For base point , power series with
Simultaneously switch the base point to
Coefficient estimation
==>
decreases with respect to
==>
let
==>
Continue, finitely many times
let
==> The power series distance at one point uniformly controls the power series distance of the region
Although this still cannot maintain the well-definedness of analytic continuation, e.g.
[analytic-space]
Net of analytic space
let be analytic, with domain
The net of
-
let
-
let and compact and transitively connected, i.e. for , there exists a construction connecting
-
forall analytic with property
domain of convergence contains ,
Net's approximation method: and
when verifying the property of the net " "
if are separated, it is necessary to construct a transitively connected containing
A possible construction method: connect with a compact polyline, such that the bounded ball of covers every point on the path, use finite covering
Power series space and analytic space deal with order differential coefficients
The order differential coefficient has basically no effect
The modification of the coefficient of a base point simultaneously acts on other base points, and does not affect the coefficient,
compare the net of analytic space vs the net of continuous function space (should be something compact open topology?)
in analytic space and its net
-
[inverse-op-continous-in-analytic-space] ==>
-
[compose-op-continous-in-analytic-space] and ==>
Or rather, the operators are continuous functions of analytic space
same for linear , multiplication , inversion ?
Example
- Affine linear
radius of convergence
The first-order term of the power series of any base point is const
A uniform distance can be defined in the affine linear space
- Polynomial mapping
radius of convergence
A uniform distance cannot be defined in the polynomial function space
[connected-analytic] in analytic space, and are in different connected components?
The properties of singularities within connected components are invariant under analytic homeomorphism
[homotopy-analytic] analytic homotopy
[power-series-analytic-equivalent] Analytic equivalent power series := Two power series come from the power series expansion of the same analytic function at different points
[power-series-analytic-homotopy-equivalent] Analytic homotopy equivalent power series := Two power series come from the power series expansion of the same homotopy class of analytic function at different points
And then we can define the non-equivalent version property between power-series