解析 (Minkowski)

为了处理的幂级数, 需要先处理值域的级数

暂时只处理类时未来的情况

[sum-preserve-time-future] let 类时未来, then 类时未来

(三角不等式)

let 类时未来 or

then 类时未来 or

, or 单调递增 [increasing-length-of-time-future-series]

let time future, not co-linear. cf. signature-of-2d-subspace-of-spacetime

通过变换, 可以假设测地线球的中心是

[sum-preserve-angle-range]

let 的方向包含在的测地线球

==> 的方向在测地线球

Proof

Question 有更直接的证明吗?

let

双曲线的测地线长度是双射. 双曲线映射到到空间轴是单射. 复合后是保持单调的双射

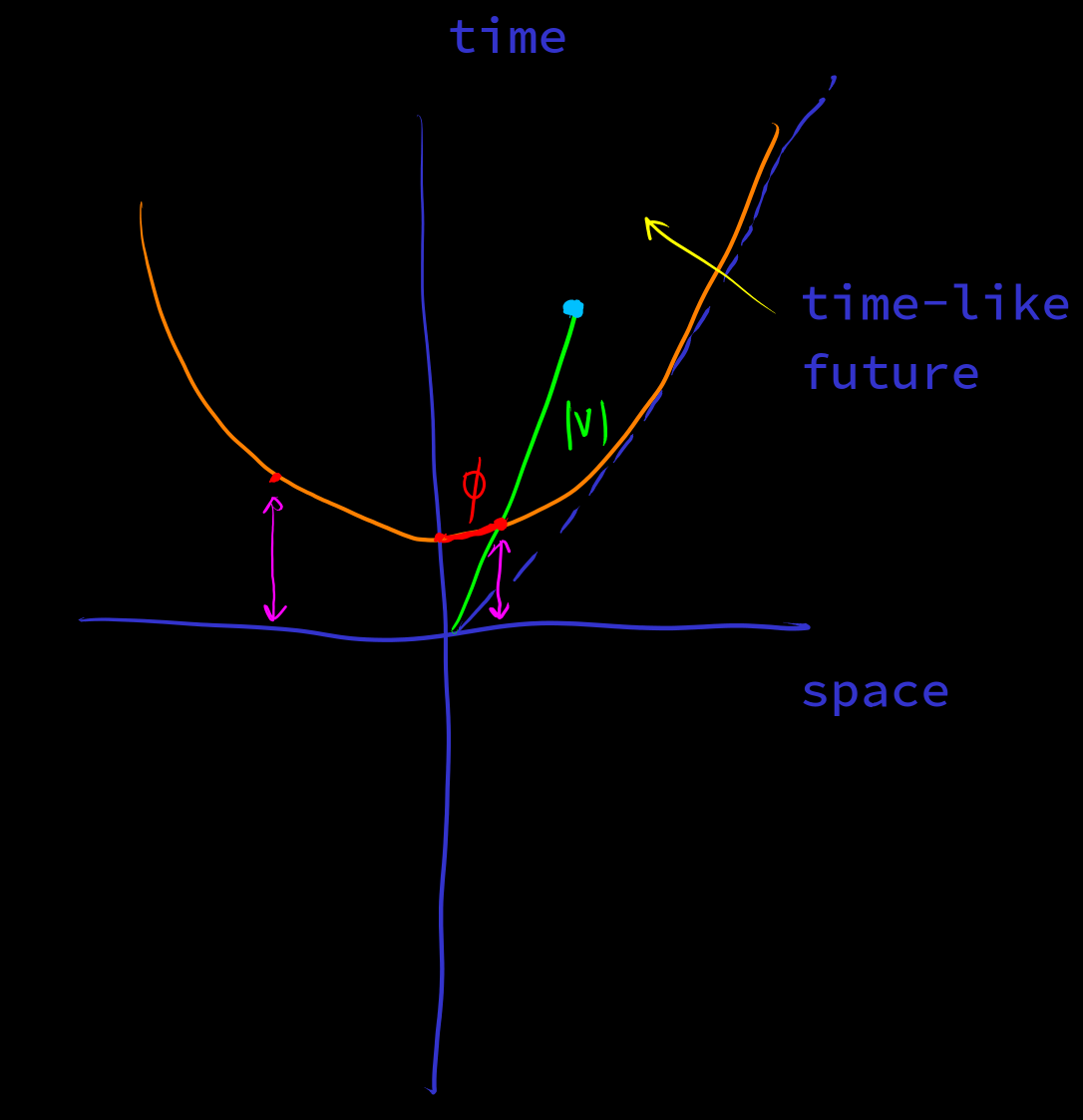
let 方向 in 测地线球

==>

Proof use signature , 嵌入 , 归纳

[quadratic-form-inequality-Minkowski-another]

let 的方向 in 测地线球

==>

Proof use cf. hyperbolic-cosine-formula

let time future, 方向在测地线球 with 半径

==> use

[absolute-convergence-Minkowski-distance] ==> 单调递增有界存在极限

[Minkowski-power-series]

let

距离极限存在 (上一个定理)
方向 , 极限存在待证明

have property

time future

称为 Minkowski 级数收敛

Proof of convergence in direction space

方向收敛

Question 有无更直接的证明

use isom-top-hyperbolic-Euclidean. 距离限制在等价于作为 Riemman manifold 的测地线距离, 两个元素相减是类空

we prove Cauchy in

==> 是 Cauchy 序列

==> all , exist , all

let

. use 两点相减是类空

use (or other) 不影响极限

use sum-preserve-time-future. 类时, . use 三角不等式 , use Cauchy

==>

==> Cauchy in

内积收敛

let
let time future
for use 双曲余弦

类时

where

未来

where

处理幂级数

let

[Minkowski-analytic] Minkowski 解析

(零阶不影响)

let 测地线坐标

目标的 property

time future ==> time future
定义范数给出绝对收敛

use 几何级数控制 like the case of Euclidean

==> and ==>

Question 类似 Euclidean 的情况, 收敛半径内蕴含 Minkowski 连续性 i.e. 距离和方向的连续, 而且有绝对一致收敛性质

Example Question

is Minkowski 解析
类似复分析, 解析 ==> Minkowski 解析
类似于 Euclidean 的情况, PDE, 特征函数, 特殊函数可能会给出更多 Minkowski-analytic 的例子

Question let Euclidean 解析 , ==> Minkowski 解析?

Question 对于 Minkowski 解析, 考虑对应到 Euclidean 的 analytic-continuation, power-series-space, analytic-space

多了 , 参数

级数 or 函数三角不等式可能需要加上参数修正的版本

解析函数空间的网的逼近时还需要作为整个方向空间的极限

note-math