[orientation-of-real-linear-space] direction
There are two directions. for vector base of , change order once change orientable, introduce a factor. This is somewhat similar to alternating-tensor. orientation defined as quotient of vector base with same orientation. equivalent to decompose of
[orientation-of-boundary-of-simplex]
simplx oriented boundary. The direction of the boundary of simplex is to define the direction for the affine subspace where the boundary is located, such that the interior is in the -dimensional positive direction and the exterior is in the -dimensional negative direction
If we continue to define the direction for the boundary of the boundary, we will find that adjacent directions cancel out
simplex vertices can construct a directed basis of according to . Permutations make the directions differ by
After selecting to be the positive direction of , the direction of the boundary is
similar to box
Example Tetrahedron, right-hand rule, with the thumb pointing towards the inside of the tetrahedron to get the boundary direction (the index of the vertices in the picture starts from instead of )
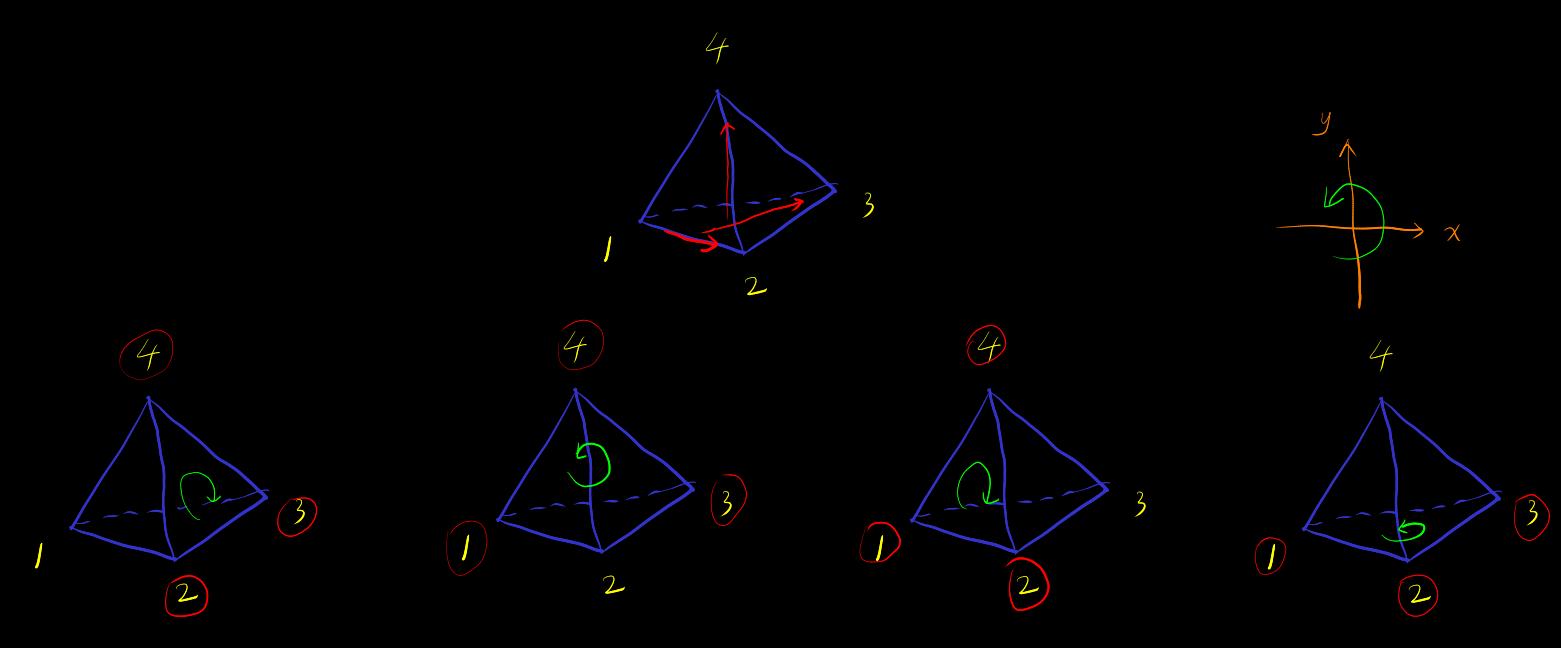
[orientable-low-dim-polyhera] Polyhedron Orientable is defined as: when constructing a polyhedron with simplexes, it is possible to define compatible orientations for all simplexes, such that the adjacent two simplexes have compatible orientations on their intersecting boundary simplexes, i.e., the orientation corresponds to the interior of simplex and the exterior of simplex . The orientation corresponds to the interior of simplex and the exterior of simplex . i.e., simplex partition has well-defined interior and exterior.
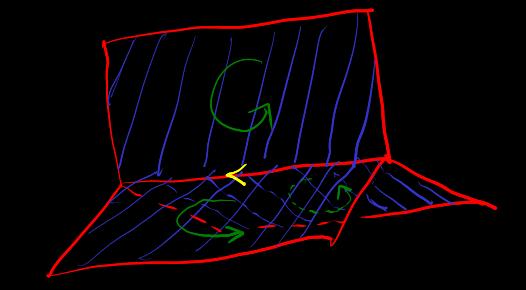
Eaxmple [Mobius-strip] Non-orientable Mobius-type polyhedron (image modified from wiki)
No matter how the direction of each simplex is defined, there exists a pair of adjacent simplex whose connected boundary simplex directions are incompatible. i.e. Simplex partitioning has no well-defined inside and outside
Starting from the initial simplex, continuously and transitively defining compatible directions for adjacent simplexes, going around in a circle will lead to incompatible directions of the connected boundary simplex. Direction corresponds to the inside of , direction corresponds to the outside of
[simplex-chain] simplex chain
[boundary-operator]
Boundary operator
boundary
Example
-
boundary-op-not-injective
-
[tri-intersect-boundary]
cycle
or
or
[simplex-homology]
k-th homology
where are in chain space
Due to geometric meaning, only coefficients are needed
[real-linear-space-trivial-homology]
is trivial homology or or in , the boundary of is zero <==> is a boundary
Try to prove it by purely affine orientation & combinatorics technique, avoid Euclidean topology
[existence-and-uniqueness-of-n-simplex-chain-with-boundary]
in , uniqueness chain of boundary
so existence of boundary of nonzero chain
and uniqueness of dim region surround by boundary
[homology-hole] For a set minus a finite number or a countable number of separated linear subspaces or polyhedra, homology is not zero
[Stokes-theorem]
Similar to the one-dimensional Fundamental Theorem of Calculus. Intuitively, divergence and the divergence theorem = high-dimensional Fundamental Theorem of Calculus
Define [exterior-differential] in coordinates, where is the volume of the coordinates, is a large class of regions, and the calculation result does not depend on the choice of coordinates.
Then there is Stokes-theorem
for orientable almost everywhere analytic manifold with boundary, or
Calculate using a box in coordinates. When all coordinates approach , it will be a partial derivative of something calculated for each coordinate axis direction. The result is , further simplification is omitted for now.
Question What is the form of the exterior derivative calculation result in the barycentric coordinates of a simplex?
However, in the proof of the one-dimensional Fundamental Theorem of Calculus, the division of a one-dimensional interval, the boundary of a one-dimensional interval, and the integral of the boundary of a one-dimensional interval are all too simple. High-dimensional regions are not that simple.
[Stokes-theorem-simple] For higher dimensions, it is difficult if it is curved. First, deal with straight things i.e. simplex or parallelepiped. The division is also the same type of region, and the boundary cancellation is also simple. Then, similar to one dimension, approximate with the Mean Value Theorem of Differential + compact control. This proves Stokes' theorem for simplex or parallelepiped.
[Stokes-theorem-proof] Question
use the approximation method used in defining integral-on-manfold
Use countable + linear approximation + partition limit that used in the definition of form integral on manifold integral-on-manfold
Approximately decompose into simplex or box, then use Stokes theorem of simplex + internal boundary cancellation, only the real boundary of manifold is left
Need to use form and integral-on-submanfold
Approximation on the boundary may require special attention. For example, approximations on boundaries shoud use simplex (box) centered on the boundary and differential at points on the boundary.
Probably need some kind of Sobolev control?
Things like the GaussโBonnet theorem of Euclidean metric manifold should also be provable using this method. Although it still needs to be considered why the result is a homology invariant Euler characteristic (off by an -dimensional Euclidean volume factor, expressed as a power of ) that is independent of the metric.
I have not deal with the Stokes theorem for manifold without boundary, have not define . Example of manifold without
Correspondence between boundary operator and exterior derivative
homology
cohomology
[coboundary-operator]
coboundary
cocycle . Intuitively, the divergence of the form at this point is zero
or
or
[de-Rham-cohomolgy] k-th de Rham cohomology
in , cohomology trivial
[cohomology-hole] form with "hole". Example in , or has a singularity at . In non- manifolds, the form and Stokes' theorem can reveal the holes in the manifold even if the function has no singularities. Example or
The case of metric manifolds
The integral of the form is equivalent to the integral of
[Hodge-star]
Hodge star operator as the orthogonal complement dual of the form
with ==>
==>
[flux]
Integral of form -> Integral of -> Integral of , interpreted as the quantity of the orthogonal complement of integrated over , i.e. flux
Represent the flux alternating tensor using the inner product duality , the inner product represents the orthogonal projection of the quantity onto the flux direction (image)
Example in Euclidean , .
- form
Coordinates
Stokes' theorem [gradient]
- form
Note that at this time, you can add a directional two-dimensional "rotation 90 degrees" to change the two-dimensional divergence into a two-dimensional curl, and the normal flux to the boundary becomes the tangent flow to the boundary.
Coordinates
Stokes' Theorem [curl]
where
- form
Coordinates
Stokes' Theorem [divergence]
in Minkowski ,