[orientation-of-real-linear-space] 方向
有两个方向. 对于 向量基, 交换一次顺序 会使得方向改变, 引入 因子. 这和交错张量有相似之处. 方向定义为基的同向 quotient, 等价于 的 分解
[orientation-of-boundary-of-simplex]
simplx 有向边界. simplex 边界 的方向是, 给边界所在的 仿射子空间定义方向, 使得内部 在 维正方向, 外部 在 维负方向
如果对边界的边界继续定义方向, 就会发现相邻方向抵消
simplex 顶点根据 可以构造 有向基. 置换使得方向相差
选取 为 正方向后, 边界的方向是
对 box 也类似
Example 四面体, 右手定则, 拇指指向四面体内部得到边界方向 (图片的顶点的指标从 而不是 开始)
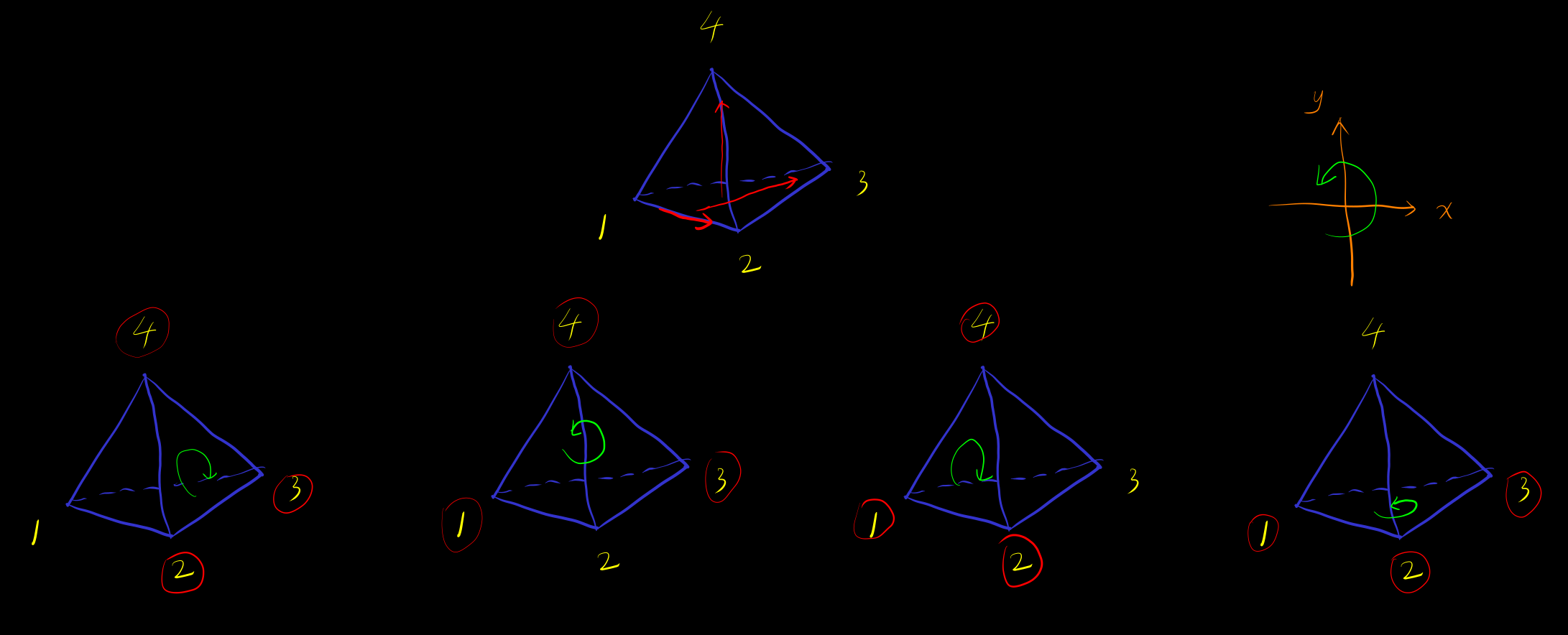
[orientable-low-dim-polyhera] 多面体 可定向 定义为, 用 simplex 构造多面体时, 能够对所有 simplex 定义兼容的方向, 使得相邻两个 simplex 的 相接边界 simplex 的方向兼容 i.e. 方向 对应 simplex 的内部和 simplex 的外部. 方向 对应 simplex 的内部和 simplex 的外部. i.e. simplex 分割有良定义内部和外部
Eaxmple [Mobius-strip] 不可定向的 Mobius 型多面体 (image modified from wiki)

不管怎么定义每个 simplex 的方向, 都存在一对相邻 simplex 的 相接边界 simplex 的方向不兼容. i.e. simplex 分割没有良定义的内部和外部
从初始 simplex 开始, 不断传递地对相邻 simplex 定义兼容的方向, 绕一圈会导致相接边界 simplex 的方向不兼容. 方向 都对应 内部, 方向 都对应 外部
[simplex-chain] simplex chain
[boundary-operator]
边界算子
boundary
Example
-
boundary-op-not-injective (p. 405 of ref-11, vol.1)
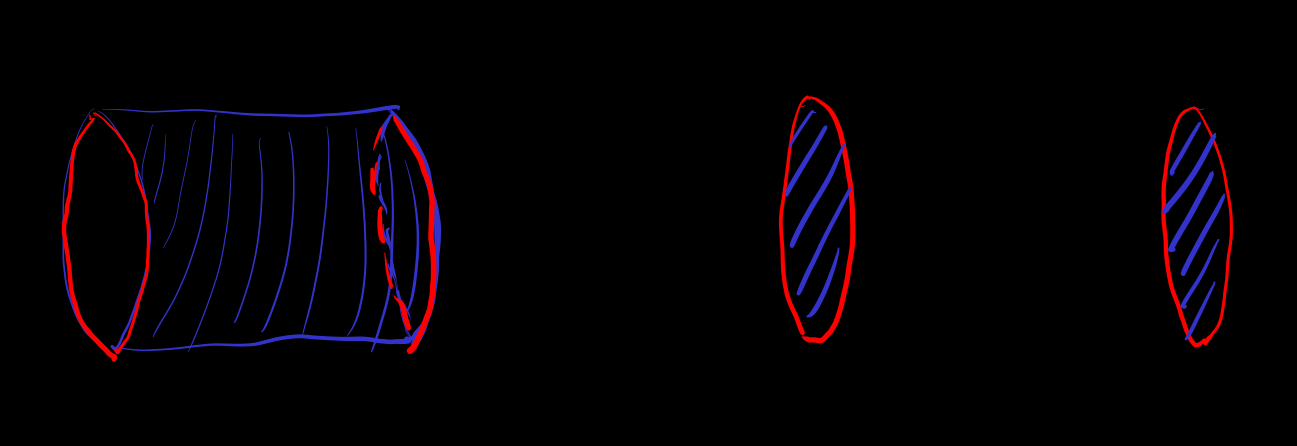

-
[tri-intersect-boundary]
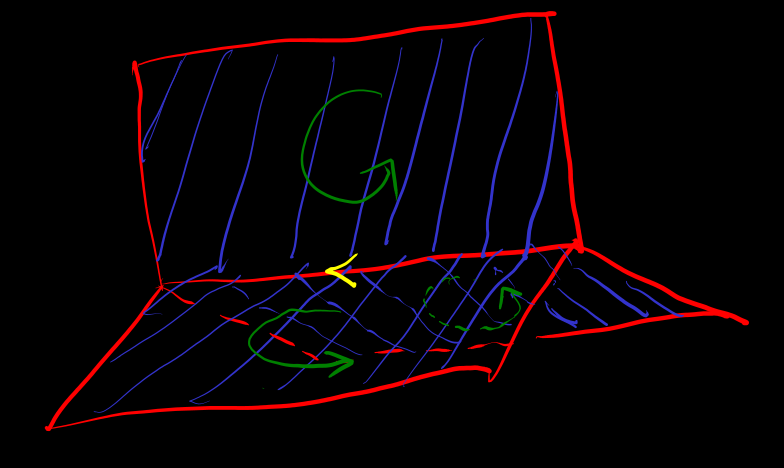
cycle
or
or
[simplex-homology]
k-th homology
where 在 chain 空间
由于几何意义, 只需要 系数
[real-linear-space-trivial-homology]
is trivial homology or or in , 的边界是零 <==> 是边界
Try to prove it by purely affine orientation & combinatorics technique, avoid Euclidean topology
[existence-and-uniqueness-of-n-simplex-chain-with-boundary]
in , uniqueness chain of boundary
so existence of boundary of nonzero chain
and uniqueness of dim region surround by boundary
[homology-hole] 对于集合 减去有限个或可数个分离的线性子空间或者多面体, homology 不是零
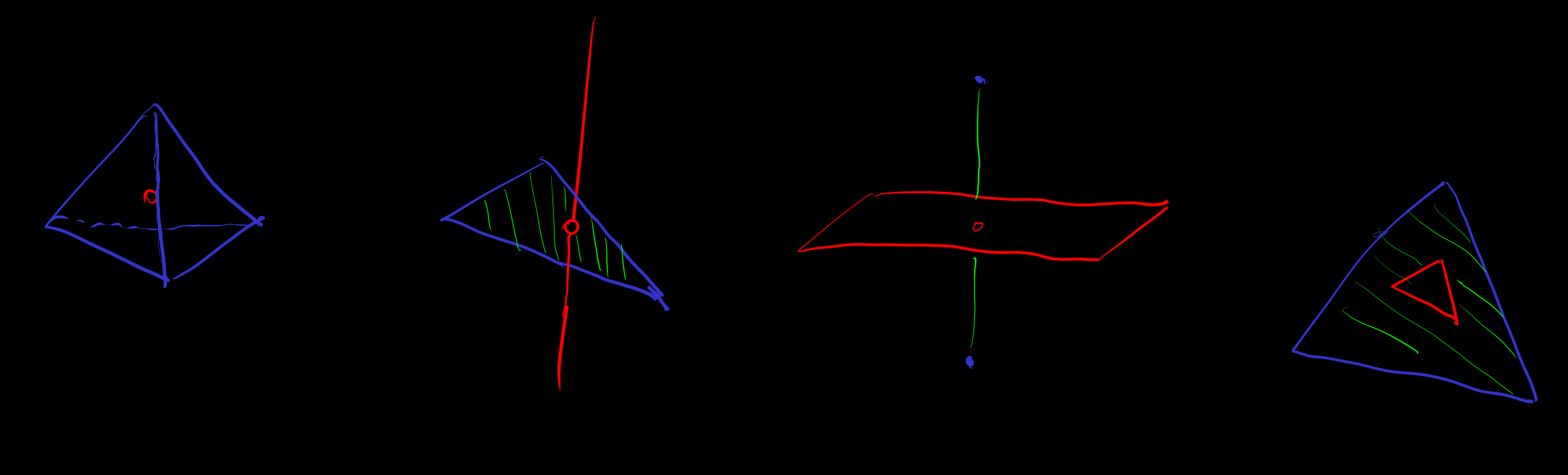
[Stokes-theorem]
类似于一维 微积分基本定理. 直观上, 散度和散度定理 = 高维微积分基本定理
在坐标里定义 [exterior-differential] , 其中 是坐标的体积, 是一大类型区域, 计算结果不依赖于坐标选取
则有 Stokes-theorem
for 可定向 的解析的带边流形和同上调零的 form, or
坐标中利用 box 计算 , 全部坐标趋于 , 将会是对每个坐标轴方向计算对某些东西的偏微分 , 结果是 , 进一步简化暂略
Question simplex 中心仿射坐标下, 外微分的计算结果的形式是什么?
但是在一维微积分基本定理的证明中, 一维区间的分割, 一维区间的边界, 一维区间的边界的积分, 都太简单了, 高维区域没那么简单
[Stokes-theorem-simple] 对于高维, 如果是弯曲的, 则很困难. 先处理直的东西 i.e. simplex or 平行体. 分割也是同类型区域, 边界抵消也很简单. 再类似于一维, 用微分中值定理近似 + compact 控制即可. 这样就证明了 simplex or 平行体的 Stokes 定理
[Stokes-theorem-proof] Question
我改变主意了. 按照直观的对流形的积分和 Stokes 定理的处理, 就应该使用将流形直接分割的方法, 而不是近似分割
积分中的分割直接可以用零阶可测集 (对微分同胚封闭). Stokes 定理中用于分割的区域应该是类似几何测度论 (ref-33) 的有限周长集 (sets of finite perimeter, Cacciopoli sets), 希望它们对有限的并集交集减集封闭, 对微分同胚封闭
证明带边流形局部是这种区域 (根据流形性质寻找多面体近似), 且这种理论的边界上的积分应该重合于流形理论中的边界上的积分 (类似几何测度论的约化边界 (reduced boundary) 理论). 证明良好的带奇点流形也属于这种区域 i.e. 多面体, 锥, 余维数 的性质良好的奇点
Stokes 定理的证明是, 用这种区域有限覆盖 form 的 compact support, 减去重复的, 分割, 然后用分割区域的 Stokes 定理, 积分在内部边界抵消, 只剩下真正的流形的边界
虽然我想回避 compact support 可微 form, 但是有些地方需要小心. 真包含链 ( 上的) 说明 form 及其外微分的 (局部) Sobolev 或者绝对连续会由于没有微分中值定理而不适合几何地定义外微分为边界积分除以体积的极限然后使用微分中值定理和重心分割几何地证明 simplex 满足 Stokes 定理. Sobolev 或绝对连续仍然对每个局部充分小的 simplex 满足 Stokes 定理. 于是如果给外微分加上有界性, 那么确实可以用积分中值来控制. 然而中值定理就是 Lipschitz 的定义 (对 simplex 体积), 而单纯的 (局部) Lipschitz 也将会蕴含几乎处处存在微分且是 (局部)
只要把 维仿射子空间看作流形 (例如在上面选取一个 基建立坐标系), 它们就有自己的体积. 选取 子空间的一个基之后, 逐点定义的 form 就能在上面变成实数值. 定义 simplex 的边界的可积至少需要 form 在每个 方向都变成可积函数. 由于 form 空间和积分的线性, 只需要对 方向空间 (对应 的 交错张量空间) 的一个基上变成可积函数, 也即被称为 "form 的分量是局部 的". 至少这种 form 在微分同胚下保持, 就如 Lebesgue 可测集那样也是在微分同胚下保持, 原则上可以说 form 在 方向导出的 子空间的函数可以被按通常积分那样由 support 在 simplex 上的分段常值函数逼近. 如果不假设可微 form, 那么我们甚至还没有定义外微分, 也没有证明 simplex 上的 Stokes 定理
尝试从积分开始定义微分, 作为结合测度和微分的一种方式. 先定义什么是满足局部无穷小 Stokes 定理的 form — 可积的可外微分 form — 再利用满足局部无穷小 Stokes 定理的 form (取代 compact support 可微 form) 去多面体逼近式地定义什么是整体满足 Stokes 定理的区域
然后用 form 的平均导数 (使用 维 simplex/box/polytope/ball 及其边界收缩到一点? 到 的最大距离 ) 来定义其外微分
接下来就需要对 simplex 证明 Stokes 定理. 用重心分割技术, 可微 form 的证明使用中值定理提供的估计
然后我们就可以尝试定义类似有限周长集的 "可以 Stokes 定理的区域" 了, 或者叫做有限周长集. 需要的限制是, 直观上, 在所有可测集中, 有一部分可测集可以进行整体 Stokes 定理的边界. 直觉上, 这种区域的限制条件应该类似于, 在逼近可测集的多面体网中存在子网良好地一致控制所有归一化或射影化的可积可外微分 form (或者其它什么更一般的东西) 在逼近多面体的边界上的积分
几何测度论中的有界变差函数和有限周长集的关系就像零阶测度论中的可积函数和可测集的关系
由于外微分只有一阶微分而不存在无穷阶外微分, 因为在 metric 流形上的 form 的 norm 就适合 Banach/Hilbert 空间理论 (无穷阶微分就不适合 Banach 空间理论)
由于流形的拓扑可能同调非平凡, 有些上同调非零的 form 的外微分 在积分时无法内部边界全部抵消, 因此会有类似于复分析中的额外的 "留数". 例如, [cohomology-hole] Example in , or , 满足 , 所以在 上积分是零, 但是 在 的边界 上的积分非零. Example 同调同构于 的
在积分时边界无法抵消的另一种例子: 原本在闭球 上成立 Stokes 定理的向量场或者 form 在删去 的边界的一个类似闭圆盘的区域后, Stokes 定理不再成立. 直观来说, 删去一个闭圆盘后, 通量就漏出来了, 说明新的边界没有封闭住流形内部. 如果不是删去闭圆盘而是删去开圆盘, 那么得到的不是带边流形, 有余维数 > 1 的边界, 且不满足边界的边界是零
可能要考虑某种 compact 约束, 因为 non-compact 带有某种无穷远使得边界抵消失败, 可能会出现留数项
像 Gauss–Bonnet 定理 of Euclidean metric manifold 这样的东西应该也可以用这种方法来证明. 虽然还需要继续考虑, 为什么结果是不受 metric 影响的 homology invariant Euler characteristic (差一个 维 Euclidean 的体积因子, 以 的幂表示)
我并没有对没有边界的流形处理 Stokes 定理, 并没有定义 . 没有的边界流形 Example
鉴于 Cantor 集构造的反例, 几乎处处解析不是处理奇点的正确方法. 尝试用删除奇点后来得到带边流形
边界算子与外微分的对应性质
homology
cohomology
[coboundary-operator]
coboundary
cocycle . 直观是这一点的 form 的散度是零
or
or
[de-Rham-cohomolgy] k-th de Rham cohomology
in , cohomology trivial
metric 流形的情况
对 form 的积分相当于对 的积分
[Hodge-star]
Hodge star 算子 as form 的正交补对偶
with ==>
==>
[flux]
对 form 积分 -> 对 积分 -> 对 积分, 解释为通过 的正交补 的量 对 积分, i.e. 通量
用 metric-dual 代表通量 交错张量, 内积代表量 在通量方向 上的正交投影
Example in Euclidean , (图)
- form
坐标
Stokes 定理 [gradient]
- form
注意此时可以加上可定向二维的 "旋转 90 度" 从二维散度变成二维旋度, 对边界的法通量变为对边界的切流量
坐标
Stokes 定理 [curl]
where
- form
坐标
Stokes 定理 [divergence]
in Minkowski ,