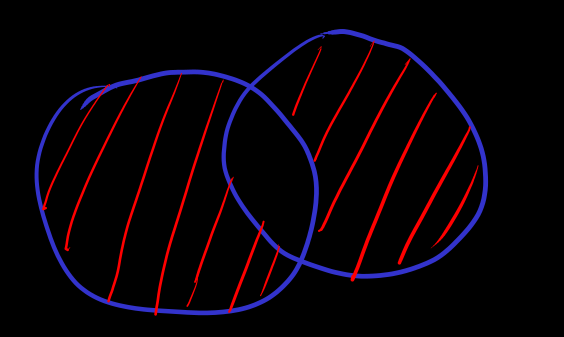
对人来说, 一种理解自然数的方式是数数 (counting)
对计算机来说 (cf. logic.typ), 表示自然数的源头是周期电路. 内存的二进制可以直接表示数字. 例如, 对于 3 bit 来说
| 二进制 | 十进制 |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
计算机的算术元件可以进行对数的 计算
还有各种更复杂的计算机行为 “递归调用自身的函数”, 也是某种数数
然而, 自然数集的元素数量是无限的, 而 bit 和计算机内存是有限的. 人类的记忆也是有限的
空间无限的问题: 现实无法构建空间无限的电路和内存. 即使能, 也受限于电流速度有限
但是可以使用潜在无限的时间来实现 “潜无限”
假设内存的上限无穷但每个周期的内存的占用都有限, 则程序有无限可能的输入, 这也是一种潜无限
理论上, 所有自然数是可以一个一个的数完的. 然而, 甚至存在集合的元素数量 不可数. 它们是无限的且数不完的. Example
- 的所有子集, or (即 映射到 的所有函数)
- 映射到自身到所有函数,
验证集合论/语言的正确性需要 parser, 或者对于数学语言来说, 也叫做 prover
集合/类型的动机
-
模块化和乘法分解以简化认知
Example 自然语言的主谓宾 SVO (subject, predicate, object). 假设有 10 个名词和 10 个动词. 假设我们 “忘记了 SVO 规则”, 那么, 验证三个词的句子的语法正确性最多需要 次. 如果理解并使用 SVO 规则, 最多需要 次
-
如果集合的元素数量是无限的, 则集合/类型将概念有限化, 使得可以在有限时间内说出来
复杂的数学对象被储存在变量名里, 所以还是需要人类去检查所有存储在变量名里面的复杂定义的正确性, 所以代码可读性很重要
prover 能让人类从需要检阅所有步骤 reduce to 检阅定义 (以及检查编译器的逻辑代码), 跳过大量详细证明步骤, 就能确定证明结果的正确性
人脑编译器能省略和补充省略, 用容易出错和遗忘来换取临时效率
除了检验证明的正确性, prover 还会有其它作用, 例如, 类似于编程语言里的工具, 可以有友好且互动的编译器错误信息, 有 LSP (language server protocol) 工具
prover 的例子: acornprover, lean
这里暂时不如进入细节, 只大概说一下
[proposition] [theorem] unproved proposition/theorem 是类型 到 的函数
theorem p(x: T) {
// ...
}
theorem p(x: T) {
// ...
}
被证明 := prover 对 的计算结果永远返回 true. 可以理解为 (通常省略 = true)
forall(x: T) {
p(x) = true
}
forall(x: T) {
p(x) = true
}
虽然我们还没有给出类型的构造规则
[set] 类型 的集合 本质上是类型 到 的函数 . 但使用一层 wrapper 有时是方便的
structure Set[K] {
contains: K -> Bool
}
structure Set[K] {
contains: K -> Bool
}
类型 的一个集合 表示为
a: Set[K]
a: Set[K]
类型 的一个元素 属于 表示为
a.contains(x)
a.contains(x)
或者
x ∈ a
x ∈ a
空集 empty[T] 对应常值 false 函数. 全集 universe[T] 对应常值 true 函数.
根据通常集合论里的 subset 的定义, 可以写为
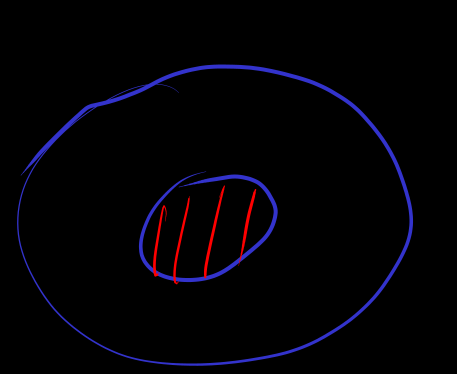
等于 可以理解为一个二元变量 Bool 函数
equal(x: T, y: T) -> Bool
满足传递性
a = b and b = c implies a = c
- forall, exists (所有, 存在)
forall(a: T) {
// ...
}
exists(a: T) {
// ...
}
forall(a: T) {
// ...
}
exists(a: T) {
// ...
}
或者写为
- inference (推导)
p implies q
p implies q
或者写为
- equivalent
p = q
p = q
或者
p iff q
p iff q
或者
(p implies q) and (q implies p)
(p implies q) and (q implies p)
或者写为
可以穷举证明以下计算结果相等
类似地, 为了表示 “无限元素” 的情况, 定义无限元素的 De Morgan law
类似 的冗余, set/type construction rules 也有可能有冗余, 或者说有很多等价的定义方式
follow 有限情况的 bool 的各种规则, 定义
[commutative-forall-exists]
same for
[distributive-forall-exists]
(需要假设函数 的存在?)
推导的自然语言例子
下雨了
所以我不会出门
这个例子类似于 conditional branch (条件分支)
let rain : bool;
let out : bool;
match (rain) {
true => out = false,
false => out = undefined,
};
let rain : bool;
let out : bool;
match (rain) {
true => out = false,
false => out = undefined,
};
类似于通常的编程语言的 if block, 在条件不满足时自动跳过执行区
if (rain = true) {
out = false
}
if (rain = true) {
out = false
}
对于数学语言, 那就是
- prover 读取到
- prover 读取到 is true (可能来自定义)
- prover 读取到 is true
- prover 根据这种条件 (来自内存), 赋予 的 bool 值为 true
如果接受类似于跳过 if block 的 “虚空蕴含”, 那么会有
并发现 就是
[reverse-inference] 反向推导. 如果结果是我出门了, 那么肯定不是下雨的结果. 如果条件分支的结果是 out = true, 这不是 rain = true 的结果. 由于理想二进制计算机的 bool 值必定二选一, 所以只能是 rain = false 的结果. 这可以被写为条件分支
match (out) {
true => rain = false,
false => rain = undefined,
};
match (out) {
true => rain = false,
false => rain = undefined,
};
数学上, 反向推导写为 formula , 并定义等价到
[natural-number]
natrual number (自然数)
natrual number set (自然数集) 是归纳类型
inductive ℕ {
0
suc(ℕ)
}
inductive ℕ {
0
suc(ℕ)
}
计算机无法处理无限. 为了让计算机能用有限的字符和内存去表示自然数集, 把 和 函数作为内存地址里的有限 symbol, 使得
等价于用指令流告诉计算机如何连续地 ? 也联系到归纳法
有限的字符的代价是潜在无限的时间, 总是借助了数数或者周期电路
定义
由于 “定义语言展开” 很长, 因此通常 abbreviated to “definition” “def”
[product]
let be set, then is set
表达式 为 product 数据结构
Abbreviation . in finite case, number of elements
[sum]
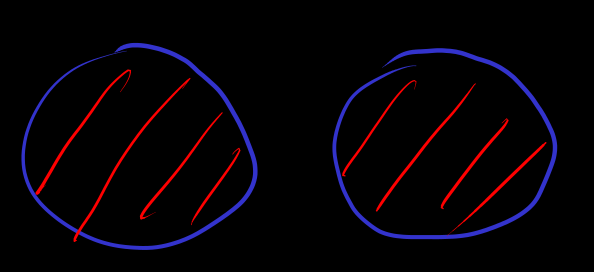
let be set then is a set
也称为 tagged union
in finite case, number of element
[function]
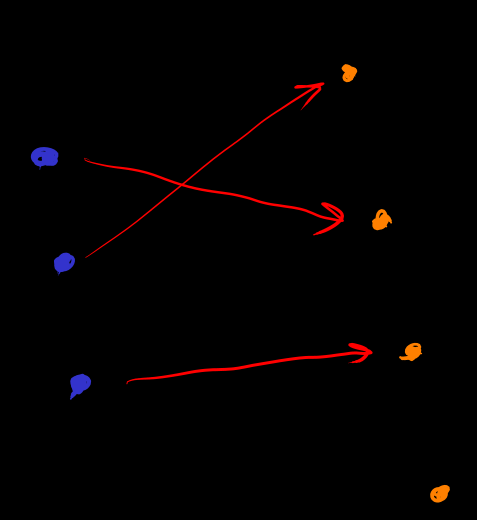
let be set. 定义 function space , map 的规则是
or
denoted by
denoted by . in finite case, number of elements
在 prover 中, 函数的定义和行为是, 输入类型 + 输出类型 + 检查到相同输入则规定输出相同
Prop . 可以对应于
[subtype]
给 type 加上一个命题然后用 logic and 可以得到 “subtype”. 它类似于 subset, 但是使用 dependent type 加了一层 wrapper
define(a: Set[K]) -> Type {
structure {
val: K
} constraint {
a.contains(val)
}
}
define(a: Set[K]) -> Type {
structure {
val: K
} constraint {
a.contains(val)
}
}
如果证明了一个关于类型 的定理, 有时候, 很容易看出它对某些子类型成立. 但是对于计算机可能要重新写一次定理. 一种减缓这种繁琐的方法是, 用 typeclass 来表示结构类型及其性质, 使得定理是基于 typeclass 的, 这样就能增加复用, 减少重复
function space 引入了高级别的无限
一件初看反直觉的事情是, 我们似乎知道所有 或所有 , 却无法数出来 cardinal-increase uncountable. 但是, “知道所有 “ 究竟是什么意思? 事实上, 试着考虑 “以一般地方式找一个 的无限子集” 这一个问题, 就会发现这不是简单的
类似地, 虽然可数已经可以定义一些实数 e.g. , 但如果不借助 or , 只有可数的构造无法得到全部
[subset]

由于 false, 根据虚空蕴含,
denoted by . in finite case, number of elements
let
或者如果 “用类型论构造集合论”, 那么集合的相等的定义 reduce to 函数 相等的定义
let
[union]
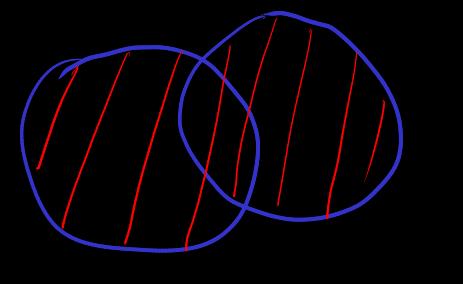
[intersection]
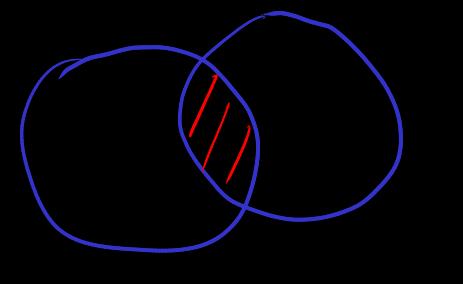
注意 union 和 intersection 的元素被限制在 type . 着通常集合论中, 如果尝试定义空集族的交集, 如果不限制在 type (或限制在某个集合), 那么由于虚空论证, 空集族的交集的结果是全集 , 而全集 不是集合, 这破坏了集合论构造规则
空集族的交集是全集的直觉: 因为交集对 是递减的, 从而交集往空集族方向不断增大
根据指标映射 可以定义无限版本的 product, sum
- [product-index]
product component
or
- [sum-index]
sum component
[hierarchy-order-of-set]
以上构造的 type/set 称为 zero (hierarchy) order type/set
or
我们可以假设
再次使用 type construction rules, 得到的东西也定义为属于
还可以继续
. 诸如此类 …
Example
-
typeclass G: Group {mul(g: G, h: G) -> Ginverse(g: G) -> G// property of group}typeclass G: Group {mul(g: G, h: G) -> Ginverse(g: G) -> G// property of group}
看起来像自然数集 , 所以应该再假设新的 hierarchy 吗? 然后对 , 继续使用 type construct rule … (会导致需要无限的语言规则吗?)
属于 且属于 , 但这两种 “属于” 的语言规则是不同
[universal-type]
universal-type 的问题, 或者 type of every type 的问题
这里的容易忽略的一点是, “type of every type” 中的 “type” 指的是什么? 所谓的 “type” 是什么意思?
假设程序定义了一种 universal-type 的概念, 且 universal-type 又可以用来构造 “type”, 则 universal-type 就自指地参与到了 “type” 的构造规则中, 导致非终结语言或程序
Example [Russell-paradox]
使用 set theory rules 定义
然后去计算另外一个命题 的 bool, 由于 = true, prover 只需计算 的 bool, 然后发现 not, 所以尝试计算 not 里面的 bool, 但这又回到了计算 的 bool, 进入电路死循环
Example [self-referential-paradox] 自指悖论. “这个句子是错的”
this_sentence_is_false : bool = false;
loop {
match (this_sentence_is_false) {
false => this_sentence_is_false = true,
true => this_sentence_is_false = false,
}
}
this_sentence_is_false : bool = false;
loop {
match (this_sentence_is_false) {
false => this_sentence_is_false = true,
true => this_sentence_is_false = false,
}
}
[dependent-distributive]
let be set of sets, let , and let be set of sets, index by its elements
union & intersection
draft of proof: 展开, 使用 distributive-forall-exists
sum & product
[set-minus]

. if then define
[symmetric-set-minus]